上一道數學謎題
下一道數學謎題
無止盡的路數學謎題
答對率:62%
「這條路走到底你就可以走出這個沙漠了。」小精靈說。
「看起來不遠嘛。」男子說。
「現在這條路有一公里長;但是這是一條有魔法的路,當你踏上去以後,每過一秒鐘這條路就會伸長一公里;會走得很累啊~ 要不要走隨便你囉。」說完小精靈就消失了。
男子想說孤注一擲,就踏上了這條路。
如小精靈所說,一秒以後,路的"全長"就變成兩公里長 ,再過一秒,全長就變成三公里長。
男子從第零秒開是走,速度是每秒走一公尺。假設他體力夠好,可以一直維持這個速度日夜不停地走。
那麼,男子有可能走到路的盡頭,離開沙漠嗎?
如果可以,大概要多久呢?
註:路是從"起點"開始「等比例」的伸長~~~
舉例來說,一秒以後路變成 2 km 時,男子已經走過的 1 m 也會等比例伸長為 2 m,所以此時他離終點有 1998 m。
再舉兩秒後的的例子:路從 1 km 變成 2km 再變成 3 km。而男子走了 2m,其中第一個 1m 最後會變成 3m (因為路從一開始是 1 km 最後是 3 km,等比例放大三倍);而第二個 1m 最後會變成 1.5 m (因為路在一秒後是 2 km 最後是 3 km,等比例放大1.5倍);所以男子走過的路一共變成 4.5 m;所以離終點還有 2995.5 m 。
看答案
走得到。但是要走很久。
P.S. 真的要很久
大概要 e1000 秒,約等於 10427 年。原因請見解析。
P.S. 真的要很久
大概要 e1000 秒,約等於 10427 年。原因請見解析。
解析
我要編輯作者:larry(岸輔 鷓) | 歷史版本
將題目轉成路的長度不變(1000m),男子的步伐變成1,1/2,1/3,1/4,...(m)。
簡單說明為何一路加下去會變無窮大:
1,1/2,1/3+1/4,1/5+1/6+1/7+1/8,1/9+...+1/16,1/17+...+1/32,...
以上用逗號分隔的每一項都大於等於1/2,因此,若項數趨近無窮大,總和亦趨近無窮大。
轉換成下圖,問題變成要有多少個矩形面積總和才會超過1000。
x>=1的部分,直接算曲線下面積,誤差不超過0.5(將多出部分當三角形即可知道)。
已知不定積分∫dx/x = ln(x) + c,假設男子要走t秒,誤差為r(0<r<0.5),
列方程式1 + ln(t) - ln(1) - r = 1000,會知道e^999<t<e^1000。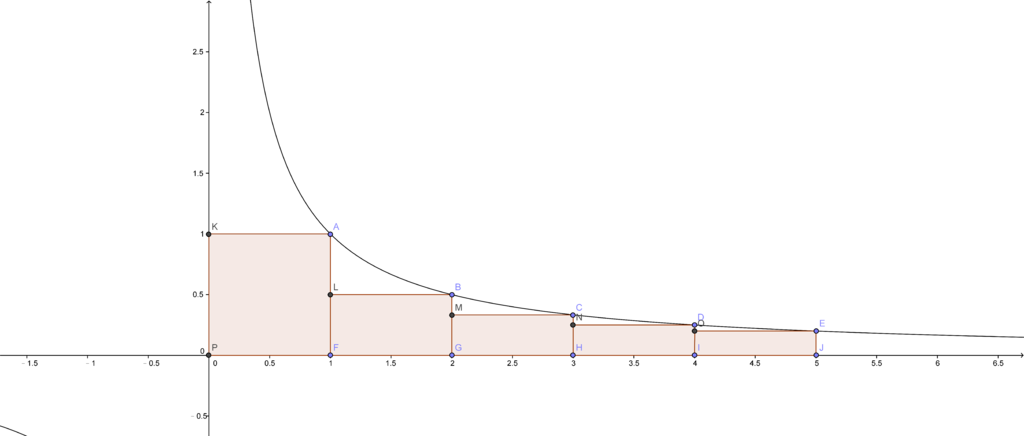
簡單說明為何一路加下去會變無窮大:
1,1/2,1/3+1/4,1/5+1/6+1/7+1/8,1/9+...+1/16,1/17+...+1/32,...
以上用逗號分隔的每一項都大於等於1/2,因此,若項數趨近無窮大,總和亦趨近無窮大。
轉換成下圖,問題變成要有多少個矩形面積總和才會超過1000。
x>=1的部分,直接算曲線下面積,誤差不超過0.5(將多出部分當三角形即可知道)。
已知不定積分∫dx/x = ln(x) + c,假設男子要走t秒,誤差為r(0<r<0.5),
列方程式1 + ln(t) - ln(1) - r = 1000,會知道e^999<t<e^1000。

4,329
上一道數學謎題
下一道數學謎題