上一道精選空間概念謎題
下一道精選空間概念謎題
翻滾吧?骰子空間概念謎題
答對率:66%
目前1點朝上,2點朝東,3點朝南。
已知骰子相對的兩面點數和為7,
並且能夠往東西南北四個方向翻滾。
並且能夠往東西南北四個方向翻滾。
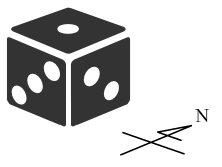
請問要達成以下目標,最少需要翻幾次?
1.停在原位,1點朝上,2點改為朝西
2.停在原位,1點朝上,2點改為朝南
看答案
1. 6次,EX:北東南南西北
2. 辦不到
2. 辦不到
解析
我要編輯作者:larry(岸輔 鷓) | 歷史版本
1.假想骰子現在正擺在棋盤格的白格子上,
翻奇數次一定會停在黑格子,偶數次則停在白格子。

翻1,3,5次會沒辦法回到原位(白格子)。
翻2次一定走原路回來,樣子不會改變。
翻4次要不走原路回來,就得繞2*2的方格,但外觀不符。
翻6次確定可行(如解答),因此6次是最少次數。
2.假想骰子現在正擺在棋盤格的白格子上,
並且把1,2,3點改為白色,4,5,6點改為黑色,
(此時相對的兩面為一黑一白)。
現在來計算看的到的面(向上、向東、向南)
以及目前的位置有幾格是黑色的:一共0格。

接著來看翻滾後會對這數量有什麼影響:
位置的黑白互換(±1),還有其中一組相對的面,
一個出現一個隱入(±1,因為是一黑一白),
數量仍維持偶數個,正是這骰子的不變量。
EX:往西再往北翻,數量依序是0+0=0,1+1=2,2+0=2



現在計算一下目標狀態的這四個位置中有幾格黑色:
總共1格(4點那面),也就是只靠翻滾是無法達成的。

翻奇數次一定會停在黑格子,偶數次則停在白格子。

翻1,3,5次會沒辦法回到原位(白格子)。
翻2次一定走原路回來,樣子不會改變。
翻4次要不走原路回來,就得繞2*2的方格,但外觀不符。
翻6次確定可行(如解答),因此6次是最少次數。
2.假想骰子現在正擺在棋盤格的白格子上,
並且把1,2,3點改為白色,4,5,6點改為黑色,
(此時相對的兩面為一黑一白)。
現在來計算看的到的面(向上、向東、向南)
以及目前的位置有幾格是黑色的:一共0格。

接著來看翻滾後會對這數量有什麼影響:
位置的黑白互換(±1),還有其中一組相對的面,
一個出現一個隱入(±1,因為是一黑一白),
數量仍維持偶數個,正是這骰子的不變量。
EX:往西再往北翻,數量依序是0+0=0,1+1=2,2+0=2



現在計算一下目標狀態的這四個位置中有幾格黑色:
總共1格(4點那面),也就是只靠翻滾是無法達成的。

14,409
上一道精選空間概念謎題
下一道精選空間概念謎題
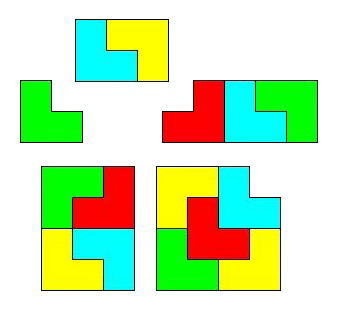 這是插曲二,和插曲一同樣是使用三連塊中的 L 。
如果 N 是一個隨意給定的正整數,
想想看該如何找...
這是插曲二,和插曲一同樣是使用三連塊中的 L 。
如果 N 是一個隨意給定的正整數,
想想看該如何找... 有一個人,他的夢想就是變成全世界最有錢的人,
一天,他走在路上突然碰到天使下凡,天使說:『我聽到你天...
有一個人,他的夢想就是變成全世界最有錢的人,
一天,他走在路上突然碰到天使下凡,天使說:『我聽到你天... 這題用正規燒繩子的方法解不出來喔!還要配合一些理想狀態下的自然方法,你想得到嗎?
桌上有好幾根繩子,...
這題用正規燒繩子的方法解不出來喔!還要配合一些理想狀態下的自然方法,你想得到嗎?
桌上有好幾根繩子,... 承昨天的題目,
有一個人,
他先往南走了1公里,
再往東走了20公里,
再往北走了1公里,
結果居然...
承昨天的題目,
有一個人,
他先往南走了1公里,
再往東走了20公里,
再往北走了1公里,
結果居然...