上一道數學謎題
下一道數學謎題
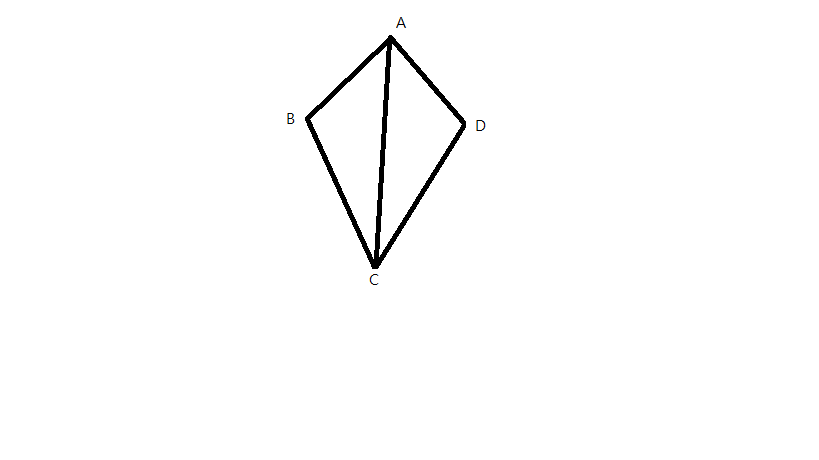
箏形土地數學謎題
答對率:68%
看答案
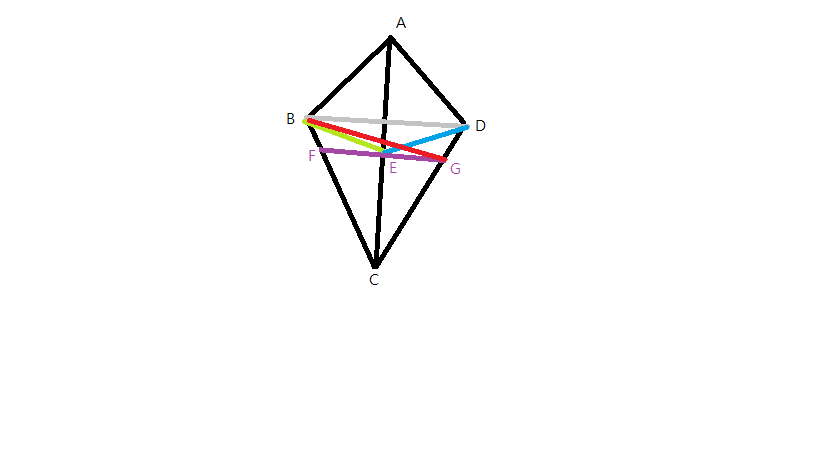
BG即為所求。
解析
我要編輯作AC中點E,連接BE及ED。
∴△BEC=1/2 △ABC
△DEC=1/2 △ADC
∴ △BEC+△DEC=1/2箏形ABCD
過E作FG平行BD交BC於F,交CD於G。
==>△BEG=△DEG(同底等高)
連接BG
1/2箏形ABCD
=△BEC+△DEC
=△BEC+△EGC+△DEG
=△BEC+△EGC+△BEG
=△BCG
--------------------------------------------------------------------------------------------
以下是直接證明:
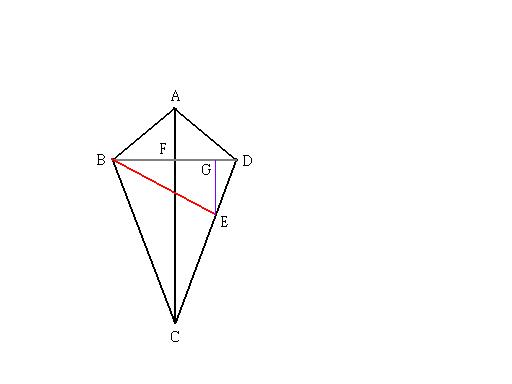
首先,假設BE將箏形ABCD面積切半且EG和BD垂直於G,所以四邊形ABED和三角形ACD面積相等
也就是 1/2 * BD * AF + 1/2 * BD * GE = 1/2 * FD * AC (1)
而 1/2 * BD = FD ,所以(1)式可簡化成 AF + GE = 1/2 * AC (2)
AC和GE都與BD垂直,所以AC和GE平行,再配合(2)式
知道E會映射到AC上的中點,因此證明完畢
∴△BEC=1/2 △ABC
△DEC=1/2 △ADC
∴ △BEC+△DEC=1/2箏形ABCD
過E作FG平行BD交BC於F,交CD於G。
==>△BEG=△DEG(同底等高)
連接BG
1/2箏形ABCD
=△BEC+△DEC
=△BEC+△EGC+△DEG
=△BEC+△EGC+△BEG
=△BCG
--------------------------------------------------------------------------------------------
以下是直接證明:

首先,假設BE將箏形ABCD面積切半且EG和BD垂直於G,所以四邊形ABED和三角形ACD面積相等
也就是 1/2 * BD * AF + 1/2 * BD * GE = 1/2 * FD * AC (1)
而 1/2 * BD = FD ,所以(1)式可簡化成 AF + GE = 1/2 * AC (2)
AC和GE都與BD垂直,所以AC和GE平行,再配合(2)式
知道E會映射到AC上的中點,因此證明完畢
5,974
上一道數學謎題
下一道數學謎題
 大家都知道,一個正方體有八個頂點;
如果從這八個頂點中隨機選出3個點,
它們連起來構成的三角形是直角...
大家都知道,一個正方體有八個頂點;
如果從這八個頂點中隨機選出3個點,
它們連起來構成的三角形是直角... 有六張V字形的卡片,都在單一面上畫了三個彩色小圓點;
六張卡片疊放在一起如下圖,
其中有兩張卡片是一...
有六張V字形的卡片,都在單一面上畫了三個彩色小圓點;
六張卡片疊放在一起如下圖,
其中有兩張卡片是一...