上一道數學謎題
下一道數學謎題
迷失方向的船 2數學謎題
答對率:72%
這個漁夫又有一天駕著一艘小船,
從一個筆直海岸的垂直方向出海,在離海岸 4 公里處捕魚。
然後很不幸地,他想要返航的時候又迷失方向了,
他趕緊查看船上的油料,可是發現所剩油料僅夠再航行 26 公里。
那麼,這次他要怎麼辦呢?

P.S. 本題與上題的差異僅在所剩油料可供航行距離限制而已,其它條件與上題相同,且分類仍屬數學謎題,所以預設答案還是很正經的。
看答案
方法可能有很多。
其中之一為稍微改良一下上題的方法即可,例如: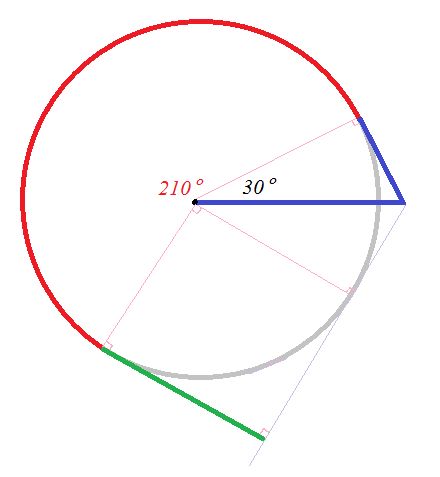
Step 1 : (藍線)
先往某一方向 (圖中為往右方) 前進 8/√3 公里。
如果沒有靠岸的話,往左轉 120 度,再往前航行 4/√3 公里。
這時候的船的位置會在:距離原本捕魚處 4 公里,且與一開始前進方向夾角為 30 度之處。
Step 2 : (紅線)
然後沿著以原本捕魚處為圓心,4 公里為半徑,逆時針航行 210 度的圓弧。
Step 3 : (綠線)
若還沒有靠岸的話,再筆直往前航行 4 公里之內必能靠岸。
用這個方法,最遠的距離為:
8/√3 + 4/√3 + 4 × (7/6)π + 4 ≈ 25.59 (km)
在 26 公里的油料限制內可以靠岸。
出本題的目的,僅是偶然有空回顧了上題,想到的一點延伸。
本題意旨並非一定要找出上題問題的最佳 (最短路徑) 解法,而是希望讀者試著稍微改變一下上次路徑,就能發現其實還有機會以更短的航行距離達成目的。
另外,我不確定以上的答案是否為本題的究極最短的航行路徑。
不過,若必須採用上題的方法 (即答案中的 藍紅綠 三段式 走法,其中 藍線不一定要是兩段直線;紅線不一定要貼著圓弧,只要頭尾兩點在圓弧上即可;綠線不一定要是直線或是圓的切線) 來航行的話,則本題的答案的方法確實是路徑最短的。
網友 bbbnnn(奇風) 提供了為何此最短路徑中,藍線與紅線交接處要由 30 度位置切入。如圖:

將圓心 (捕魚處) 沿著一條切線 (最晚可能碰到的海岸線) 鏡射到一點。這樣,解答中的 Step 1 的兩段直線,長度就相當於 鏡射點到切線上 再到 圓上的切點。這兩段線的長度若要最短,就是如右圖中剛好連成一直線的時候。此時,不難看出圖中的直角三角形都是 30°-60°-90° 的,故切入圓弧的最佳位置即是與一開始出發前進方向夾 30 度之處。
至於為什麼最短路徑中:藍線接紅線要由沿著切線切入、紅線要貼著圓弧、紅線接綠線要沿切線方向切出、綠線要垂直最晚可能碰到的海岸線,這些問題,有興趣的朋友可以自行證明看看。
再延伸一題好了…
又有一天,這個漁夫想要抓些深海大魚,
所以這次他改成駕駛潛水艇去捕魚,
他航行到離岸足夠遠,海底也足夠深的汪洋中,
然後從海平面垂直下潛 4 公里,開始捕魚。
很不幸地,他要返航的時候又迷失方向了,
並且一如往常,潛水艇上該壞的都壞了,
沒有燈光,沒有水平儀,也無法靠水壓得知水深,
而且艦身的質量分布頗均勻,且其密度與海水一樣
(抽水裝置壞了,無法進水或排水改變密度),
也就是說,潛水艇本身不會上浮或下沉,也不會因為某側較重而翻轉,
無法靠潛水艇本身的運動來判斷方向。
完全只能靠推進器來和他過人的航海操控能力來控制行進方向的 上下、左右、前後。
他趕緊查看艦上的油料,雖然還足夠航行一段距離,但仍不能浪費。
而真正要命的是,他發現艦上的氧氣供給量所剩非常有限!
因此他必須盡快地駛出水面。
那麼,這次他要怎麼辦呢?
其中之一為稍微改良一下上題的方法即可,例如:

Step 1 : (藍線)
先往某一方向 (圖中為往右方) 前進 8/√3 公里。
如果沒有靠岸的話,往左轉 120 度,再往前航行 4/√3 公里。
這時候的船的位置會在:距離原本捕魚處 4 公里,且與一開始前進方向夾角為 30 度之處。
Step 2 : (紅線)
然後沿著以原本捕魚處為圓心,4 公里為半徑,逆時針航行 210 度的圓弧。
Step 3 : (綠線)
若還沒有靠岸的話,再筆直往前航行 4 公里之內必能靠岸。
用這個方法,最遠的距離為:
8/√3 + 4/√3 + 4 × (7/6)π + 4 ≈ 25.59 (km)
在 26 公里的油料限制內可以靠岸。
出本題的目的,僅是偶然有空回顧了上題,想到的一點延伸。
本題意旨並非一定要找出上題問題的最佳 (最短路徑) 解法,而是希望讀者試著稍微改變一下上次路徑,就能發現其實還有機會以更短的航行距離達成目的。
另外,我不確定以上的答案是否為本題的究極最短的航行路徑。
不過,若必須採用上題的方法 (即答案中的 藍紅綠 三段式 走法,其中 藍線不一定要是兩段直線;紅線不一定要貼著圓弧,只要頭尾兩點在圓弧上即可;綠線不一定要是直線或是圓的切線) 來航行的話,則本題的答案的方法確實是路徑最短的。
網友 bbbnnn(奇風) 提供了為何此最短路徑中,藍線與紅線交接處要由 30 度位置切入。如圖:

將圓心 (捕魚處) 沿著一條切線 (最晚可能碰到的海岸線) 鏡射到一點。這樣,解答中的 Step 1 的兩段直線,長度就相當於 鏡射點到切線上 再到 圓上的切點。這兩段線的長度若要最短,就是如右圖中剛好連成一直線的時候。此時,不難看出圖中的直角三角形都是 30°-60°-90° 的,故切入圓弧的最佳位置即是與一開始出發前進方向夾 30 度之處。
至於為什麼最短路徑中:藍線接紅線要由沿著切線切入、紅線要貼著圓弧、紅線接綠線要沿切線方向切出、綠線要垂直最晚可能碰到的海岸線,這些問題,有興趣的朋友可以自行證明看看。
再延伸一題好了…
又有一天,這個漁夫想要抓些深海大魚,
所以這次他改成駕駛潛水艇去捕魚,
他航行到離岸足夠遠,海底也足夠深的汪洋中,
然後從海平面垂直下潛 4 公里,開始捕魚。
很不幸地,他要返航的時候又迷失方向了,
並且一如往常,潛水艇上該壞的都壞了,
沒有燈光,沒有水平儀,也無法靠水壓得知水深,
而且艦身的質量分布頗均勻,且其密度與海水一樣
(抽水裝置壞了,無法進水或排水改變密度),
也就是說,潛水艇本身不會上浮或下沉,也不會因為某側較重而翻轉,
無法靠潛水艇本身的運動來判斷方向。
完全只能靠推進器來和他過人的航海操控能力來控制行進方向的 上下、左右、前後。
他趕緊查看艦上的油料,雖然還足夠航行一段距離,但仍不能浪費。
而真正要命的是,他發現艦上的氧氣供給量所剩非常有限!
因此他必須盡快地駛出水面。
那麼,這次他要怎麼辦呢?
7,028
上一道數學謎題
下一道數學謎題
 情人節那天,張先生約好要和交往中的女同事去吃晚餐,下班後坐在辦公室等她。但她遲遲沒有出現,打電話也沒...
情人節那天,張先生約好要和交往中的女同事去吃晚餐,下班後坐在辦公室等她。但她遲遲沒有出現,打電話也沒...