上一道精選創造力謎題
下一道精選創造力謎題
正方形紙片創造力謎題
答對率:54%

(1) 24 cm × 16 cm 的長方形
(2) 40 cm × 23 cm 的長方形
(3) 76 cm × 75 cm 的長方形
(4) 13 cm × 11 cm 的長方形
那麼,以上的長方形 最少各需用幾張紙片才能拼成呢?
歡迎留言答案
(PS 我不確定我自己答案一定是最少的,所以只要有哪位的答案比我的更少,並且紙片排法正確,答案就會更新為更少的。)
新增第四題,改成數字小一點的…
(4) 13 cm × 11 cm 的長方形
那麼,以上的長方形 最少各需用幾張紙片才能拼成呢?
歡迎留言答案
(PS 我不確定我自己答案一定是最少的,所以只要有哪位的答案比我的更少,並且紙片排法正確,答案就會更新為更少的。)
新增第四題,改成數字小一點的…
看答案
(1) 3 片
(2) 9 片
(3) 11 片 (不確定能否更少)
(4) 6 片
(2) 9 片
(3) 11 片 (不確定能否更少)
(4) 6 片
解析
我要編輯這個題目大概會用到幾招:
A) 邊長有公因數可提出,視為長寬為最簡單整數比的長方形。(可簡化問題,但不敢保證一定會最少)
B) 拿可容許的最大正方形 (邊長等於長方形的短邊長) 來拼,剩下的面積 (也是長方形) 也繼續用同一招來拼。(這就是諸位有提到的輾轉相除法)
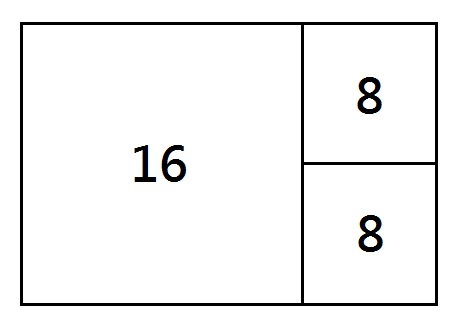
如題 (1),用 A 招當作 3 × 2 的長方形,再用 B 招即可輕易拼出 (圖中數字為正方形邊長,以下皆同):
題 (2) 的長方形邊長互質不能用 A 招,所以重覆用 B 招幾次。不過,當剩下一個 6 × 5 的小長方形時,若還是用 B 招,則需要再 6 片正方形來拼;但若是如下圖 (粉紅色區) 拼法,則只需 5 片。故題 (2) 總共用 9 片:
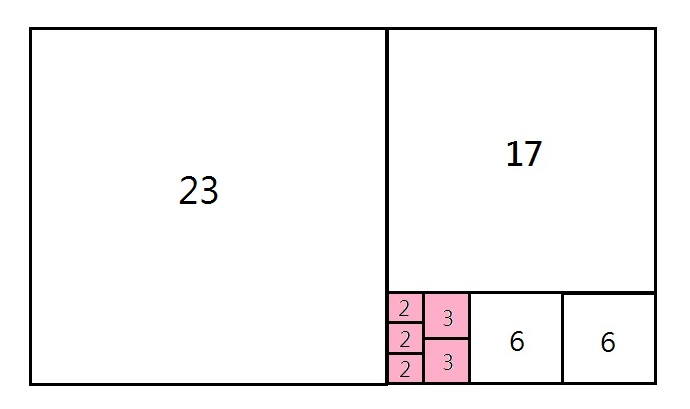
C) 由上可發現,並不一定要盲從 B 招;有時讓長方形邊長為合數的那一邊 (上例 6 × 5 的 6),用兩片以上 (看它是幾的倍數就用幾片,上例為兩片 邊長為 3 的正方形) 正方形來拼,剩下的長方形 (上例為 6 × 2) 的邊長反而有公因數,就可以用 A 招。這樣有可能比完全用 B 招用的正方形來得少片。
如題 (3),全用 B 招的話要用七十多片,故考慮用 C 招。因為長寬都是合數,所以就都試試看吧~ 解如下圖:
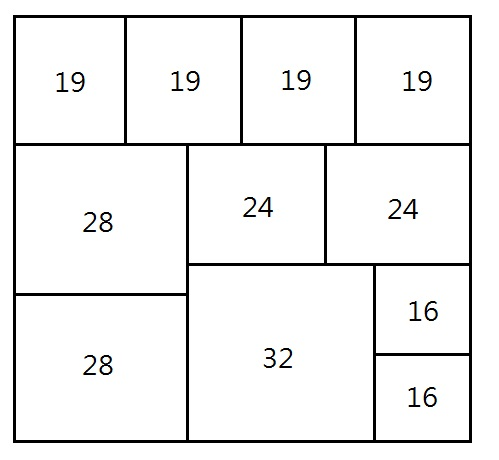
注意到先用 4 片 邊長為 19 的正方形以後,剩下的長方形為 56 × 76 ,可以用 A 招化簡;而之後又反覆使用 C 招兩次 (而非 B 招!)。最後剩 48 × 32 的長方形,用 A 招回到題 (1) 。
題 (4),邊長都是質數,A、C 招都不能用。全用 B 招的話,需要 8 片正方形。但實際上用 D 招,最少只要 6 片:
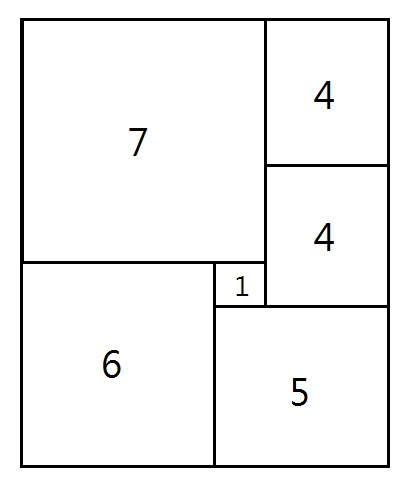
D) 有的題目剛好就有這麼巧的解,要有創意和毅力才能得到…
更誇張一點的用 D 招的題目,已出現在遊戲學校過: http://gameschool.cc/puzzle/249/ (這一題甚至每個正方形的邊長都不一樣。如果允許用一樣的,可能可以更少?!)
總之,這個題目沒有想像中簡單,一成不變的方法常常行不通的 ^O^ ~
P.S. 為了這題我寫了程式代碼,請電腦幫忙驗算;可是計算量太大電腦也算不出來 (或許是我的代碼不夠好吧),像 題(3) 長方形的邊長太大,算不出來,我不敢保證以上的方法一定最少。 但是 題 (1) (2) (4) 解答應該都是最少的 (電腦 check 過沒問題)。
A) 邊長有公因數可提出,視為長寬為最簡單整數比的長方形。(可簡化問題,但不敢保證一定會最少)
B) 拿可容許的最大正方形 (邊長等於長方形的短邊長) 來拼,剩下的面積 (也是長方形) 也繼續用同一招來拼。(這就是諸位有提到的輾轉相除法)
如題 (1),用 A 招當作 3 × 2 的長方形,再用 B 招即可輕易拼出 (圖中數字為正方形邊長,以下皆同):

題 (2) 的長方形邊長互質不能用 A 招,所以重覆用 B 招幾次。不過,當剩下一個 6 × 5 的小長方形時,若還是用 B 招,則需要再 6 片正方形來拼;但若是如下圖 (粉紅色區) 拼法,則只需 5 片。故題 (2) 總共用 9 片:

C) 由上可發現,並不一定要盲從 B 招;有時讓長方形邊長為合數的那一邊 (上例 6 × 5 的 6),用兩片以上 (看它是幾的倍數就用幾片,上例為兩片 邊長為 3 的正方形) 正方形來拼,剩下的長方形 (上例為 6 × 2) 的邊長反而有公因數,就可以用 A 招。這樣有可能比完全用 B 招用的正方形來得少片。
如題 (3),全用 B 招的話要用七十多片,故考慮用 C 招。因為長寬都是合數,所以就都試試看吧~ 解如下圖:

注意到先用 4 片 邊長為 19 的正方形以後,剩下的長方形為 56 × 76 ,可以用 A 招化簡;而之後又反覆使用 C 招兩次 (而非 B 招!)。最後剩 48 × 32 的長方形,用 A 招回到題 (1) 。
題 (4),邊長都是質數,A、C 招都不能用。全用 B 招的話,需要 8 片正方形。但實際上用 D 招,最少只要 6 片:

D) 有的題目剛好就有這麼巧的解,要有創意和毅力才能得到…
更誇張一點的用 D 招的題目,已出現在遊戲學校過: http://gameschool.cc/puzzle/249/ (這一題甚至每個正方形的邊長都不一樣。如果允許用一樣的,可能可以更少?!)
總之,這個題目沒有想像中簡單,一成不變的方法常常行不通的 ^O^ ~
P.S. 為了這題我寫了程式代碼,請電腦幫忙驗算;可是計算量太大電腦也算不出來 (或許是我的代碼不夠好吧),像 題(3) 長方形的邊長太大,算不出來,我不敢保證以上的方法一定最少。 但是 題 (1) (2) (4) 解答應該都是最少的 (電腦 check 過沒問題)。
5,925
上一道精選創造力謎題
下一道精選創造力謎題
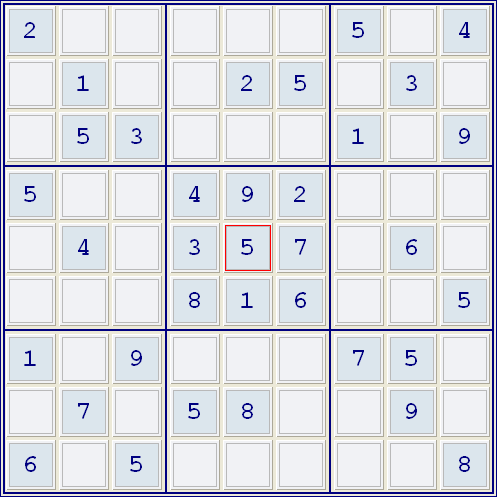 數獨遊戲中,一開始給的數字越多,就會越容易解嗎?試試看以下的題目吧。
請完成以下數獨:
解出的朋友,...
數獨遊戲中,一開始給的數字越多,就會越容易解嗎?試試看以下的題目吧。
請完成以下數獨:
解出的朋友,... 有ABCD四個種族的人,要坐在下面這八張椅子上:
其中:
每個種族至少有一個人,C族只有一個人
A...
有ABCD四個種族的人,要坐在下面這八張椅子上:
其中:
每個種族至少有一個人,C族只有一個人
A... 這究竟是由幾張照片合成的?
還有你為何會如此認為呢?
這究竟是由幾張照片合成的?
還有你為何會如此認為呢? 黃老爹很愛抽菸,家人朋友都一直勸他要戒菸,
某天,他宣布自己要戒菸了,並保證說:『我絕不戒第二次菸』...
黃老爹很愛抽菸,家人朋友都一直勸他要戒菸,
某天,他宣布自己要戒菸了,並保證說:『我絕不戒第二次菸』...