上一道精選空間概念謎題
下一道精選空間概念謎題
剪色紙空間概念謎題
答對率:61%
給你一張正方形的色紙1
和一把鋒利的剪刀2

請將色紙完整對折3兩次
然後剪上一刀4
讓色紙分成四片5
注釋:
- 色紙就是你知道的那種色紙;正方形就是你知道的那種正方形。
- 剪刀鋒利表示可以一刀兩斷,其切面會是一個理想的平面。
- 「完整對折」指的是沿色紙的某一條線對稱軸對折,理想狀況下對折的兩半應完全重疊。至於那兩次各要沿哪一條對稱軸對折則可自由選擇,沒有限制。
- 只能剪一條直線,不能轉彎;且要快速果斷,不能磨磨蹭蹭地慢慢用刀鋒去鋸色紙。
- 分成四片的色紙大小不需相同;不過必須是被剪刀剪的那一刀分開的才算數,亦即用手撕、用其它工具或其他原因使色紙破裂分開皆不可行。
- 還有哪裡看不懂嗎…
看答案
基本上,只有一種方法(類似的算同一種);即平行色紙的其中一邊,同方向對折兩次(摺線不交叉),形成一個細長的長方形,並剪去一角。如圖:
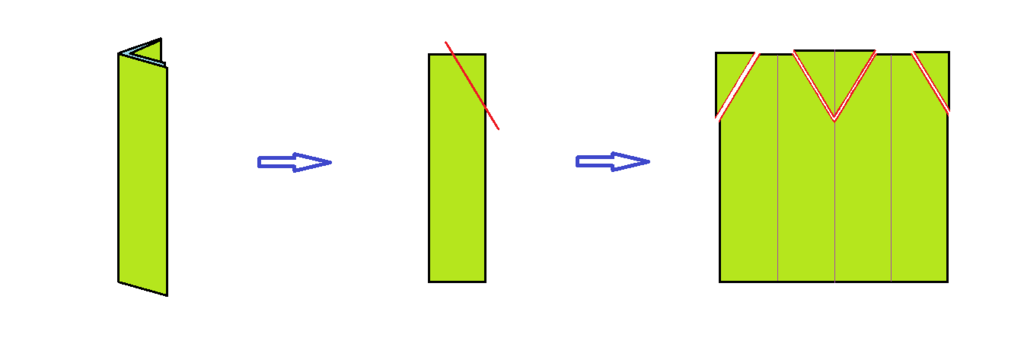
即可將分色紙分成 4 片。
在剪刀鋒利和對完整對折的「理想」情況下,使用其它的折法幾乎不可能做到剪一刀切成 4 片。

即可將分色紙分成 4 片。
在剪刀鋒利和對完整對折的「理想」情況下,使用其它的折法幾乎不可能做到剪一刀切成 4 片。
解析
我要編輯在剪刀和折紙都是「理想」的情況下,看似應該有另一種方法能做到:
對折的兩次摺線垂直交叉,使色紙形成一個小正方形(或小的等腰直角三角形),然後剪一刀通過其中一個角(為整張色紙的中心),應該就能將色紙分成 4 片…
可惜這麼做,最後極有可能只有 3 片而已,可以實際拿紙來剪剪看。如下圖:
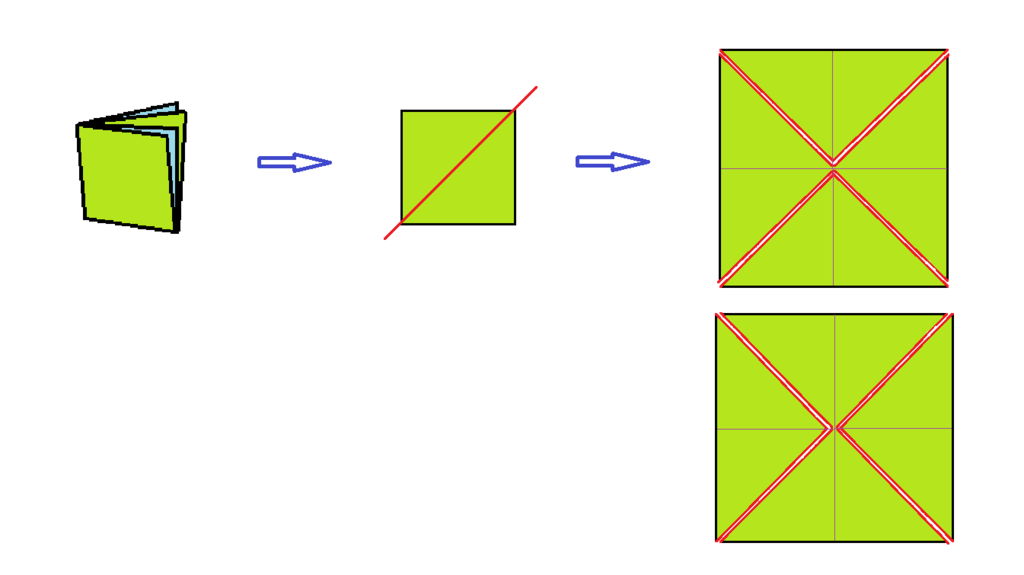
如圖,其中「兩片」仍會有一小部分仍接合著,故其實總共只有 3 片而已。(一開始對折兩次成小三角形也是一樣,剪出來的結果應似有 4 片方形,但其中「兩片」的一角仍會接合著。)
這個方法不好的關鍵在於,你必須「完全剛好」剪中色紙的中心點才能成功!但是一個點是沒有面積的 ,因此這樣成功的機率微乎其微。剪刀和折紙都是「理想」的,但是剪的人不是!
(或許你能剪得夠準,讓那「兩片」的接合處很小,輕輕一點外力或重力就會斷裂,而使結果有 4 片;但是那樣就不算是你剪一刀造成的了。)
那麼,在這樣的折法之下,有沒有其它剪法呢?

如上圖,這樣剪最後將分出 5 片。
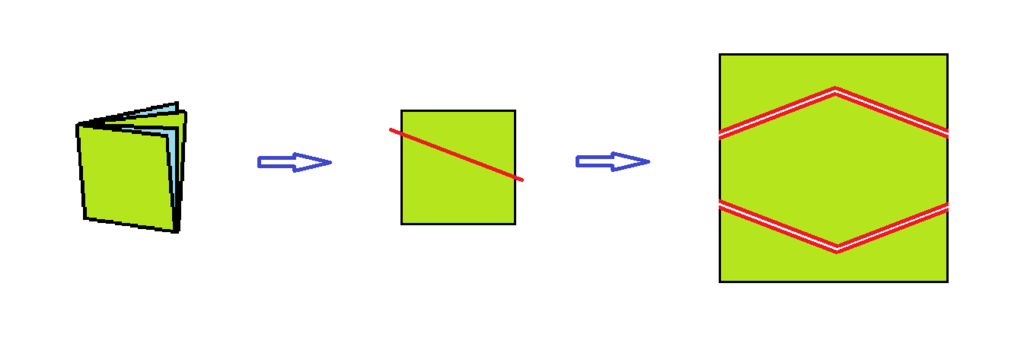
如上圖,這樣剪最後將分出 3 片。
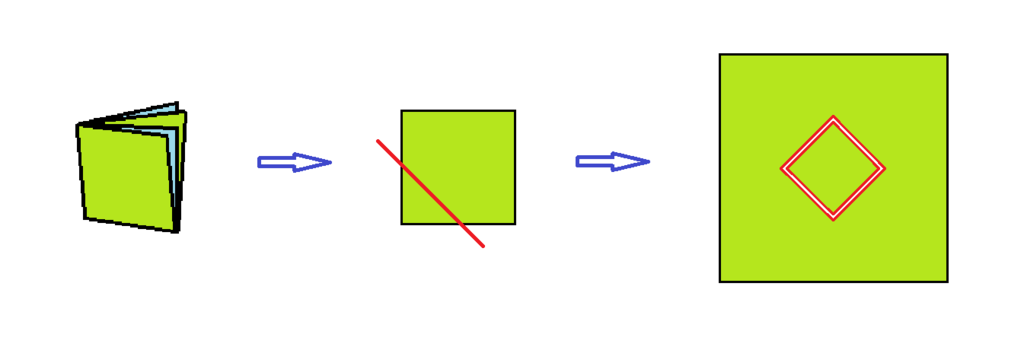
如上圖,這樣剪最後將分出 2 片。
很遺憾,在這樣的兩次對折之後,沒有能夠一刀剪出 4 片的(且成功率夠高的)方法。
對折的兩次摺線垂直交叉,使色紙形成一個小正方形(或小的等腰直角三角形),然後剪一刀通過其中一個角(為整張色紙的中心),應該就能將色紙分成 4 片…
可惜這麼做,最後極有可能只有 3 片而已,可以實際拿紙來剪剪看。如下圖:

如圖,其中「兩片」仍會有一小部分仍接合著,故其實總共只有 3 片而已。(一開始對折兩次成小三角形也是一樣,剪出來的結果應似有 4 片方形,但其中「兩片」的一角仍會接合著。)
這個方法不好的關鍵在於,你必須「完全剛好」剪中色紙的中心點才能成功!但是一個點是沒有面積的 ,因此這樣成功的機率微乎其微。剪刀和折紙都是「理想」的,但是剪的人不是!
(或許你能剪得夠準,讓那「兩片」的接合處很小,輕輕一點外力或重力就會斷裂,而使結果有 4 片;但是那樣就不算是你剪一刀造成的了。)
那麼,在這樣的折法之下,有沒有其它剪法呢?

如上圖,這樣剪最後將分出 5 片。

如上圖,這樣剪最後將分出 3 片。

如上圖,這樣剪最後將分出 2 片。
很遺憾,在這樣的兩次對折之後,沒有能夠一刀剪出 4 片的(且成功率夠高的)方法。
15,726
上一道精選空間概念謎題
下一道精選空間概念謎題
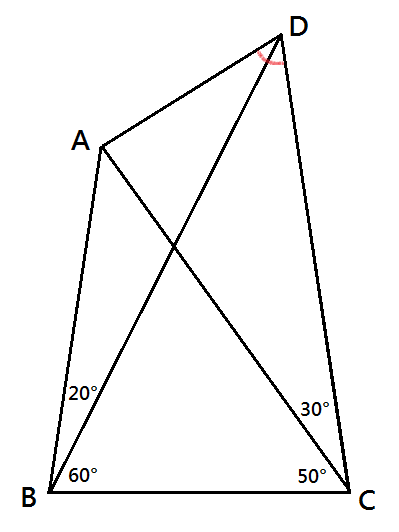 如圖,有一個四邊形 ABCD 。其中 ∠ABD = 20° ,∠CBD = 60° ,∠ACD =...
如圖,有一個四邊形 ABCD 。其中 ∠ABD = 20° ,∠CBD = 60° ,∠ACD =... (續集,應該比較簡單。)
有另一塊草坪,形狀也是正三角形的。草坪中 (不是正中央) 插了一枝旗子。
...
(續集,應該比較簡單。)
有另一塊草坪,形狀也是正三角形的。草坪中 (不是正中央) 插了一枝旗子。
... 十二月的五星難題公佈啦!! 快來挑戰吧!
小金逛街時看到一個奇怪的攤子,攤子上只放了一小堆糖果,
小...
十二月的五星難題公佈啦!! 快來挑戰吧!
小金逛街時看到一個奇怪的攤子,攤子上只放了一小堆糖果,
小...