上一道精選創造力謎題
下一道精選創造力謎題
六積木秤重--三部曲之四(?)創造力謎題
答對率:67%
有三個50克重跟三個40克重的積木,
它們全部被漆成了綠色,
六個積木從外觀都分不出來哪個是50克重,哪個是40克重。
現在有一個磅秤,限重200克,
請問你至少要秤幾次,才可以分出這六個積木各自的重量呢?

看答案
四次。
五次以上一定有解。(就算一次稱一個,最後一個不用稱,也只要五次。)
兩次以下不會有解,因為稱一次重最多得到 4 種結果 (即一次稱三個積木,結果可能是 120, 130, 140, 150 g),稱兩次 "理想上" 最多可分別 4 × 4 = 16 種結果;而六塊積木的重量共有 C(6,3) = 20 種可能性,稱兩次必然不夠。
然後很遺憾地,稱三次也沒有解;至少仍要稱四次(如解析)。
五次以上一定有解。(就算一次稱一個,最後一個不用稱,也只要五次。)
兩次以下不會有解,因為稱一次重最多得到 4 種結果 (即一次稱三個積木,結果可能是 120, 130, 140, 150 g),稱兩次 "理想上" 最多可分別 4 × 4 = 16 種結果;而六塊積木的重量共有 C(6,3) = 20 種可能性,稱兩次必然不夠。
然後很遺憾地,稱三次也沒有解;至少仍要稱四次(如解析)。
解析
我要編輯解析著重於證明僅稱三次是沒有解的。
先注意到,一次稱 1 塊積木最多可得 2 種結果 (40, 50 g),2 塊積木最多可得 3 種結果 (80, 90, 100 g),3 塊積木最多可得 4 種結果 (120, 130, 140, 150 g);而因為六塊積木總重已知,稱 4 塊與稱 2 塊一樣最多只有 3 種結果,稱 5 塊和 稱 1 塊一樣。
現在令目標是最多稱三次;六塊積木分別編號 A~F。
如果第一次僅稱 1 塊積木,那麼會是無解的。因為第一次稱完後,剩下的 5 塊重量分配有 C(5,2)=10 種可能性;但是之後從這剩下的 5 塊中即使拿 3 塊來稱,最多只可得 3 種結果 (而非 4 種,因為會少掉一種三塊等重,即 120 g 或 150 g 的結果);如今僅剩兩次可稱,最多僅可得到 3×3=9 種結果,不夠分別剩下的 10 種可能性。
如果第一次稱 2 塊積木:假設稱 A+B
先介紹我記錄稱重過程的格式,之後的記錄會此依格式作簡寫,較為清楚且便利。
第 1 次} 稱 A+B
結果= 80 克] (在此結果下,積木的重量共有 4 種可能,如右) [AB(C|D|E|F),] (中括號用來列出六塊積木重量的可能性:"[,]"內逗號左邊是是 40 g ,右邊的是 50 g ;而 (C|D|E|F) 表示可能為 C,D,E,F 其中一塊。只要 40 或 50 g 有一邊寫滿三塊,另一邊亦可得知,故省略之)
結果=100 克] (在此結果下,積木的重量共有 4 種可能,如右) [,AB(C|D|E|F)]
結果= 90 克] (在此結果下,積木的重量共有 12 種可能,如右) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
接下來想第二次要怎麼稱。在這之前,以簡寫方式記錄,把第一次稱的結果記錄繼續加寫, 比較清楚:
1} A+B
=080] (4) [AB(C|D|E|F),]
2}
=100] (4) [,AB(C|D|E|F)]
2}
=090] (12) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
2}
先想第一次得出結果是 80 g 的話,第二次該怎麼稱。因為已知 A,B 了,剩下的 C~F 還有 4 種可能,而此時從 C~F 中選 2 塊稱的話,只會有 2 種結果 (90 或 100 g,而非 3 種),假設稱 C+D ,那麼可得:
1} A+B
=080] (4) [AB(C|D|E|F),]
2} C+D
=090] (2) [ABC,] [ABD,]
3}
=100] (2) [ABE,] [ABF,]
3}
=100] (4) [,AB(C|D|E|F)]
2}
=090] (12) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
2}
觀察以上,發現第二次稱得結果分別是 90 或 100 g 時,第三次分別稱 C 或 E 即可分辨所有方塊。
同理,當第一次得出結果是 100 g 的話,第二、第三次也可以類似的方法得出。記錄如下:
1} A+B
=080] (4) [AB(C|D|E|F),]
2} C+D
=090] (2) [ABC,] [ABD,]
3} C
=040] (1) [ABC] # (打井號表示六塊積木重量全都得知了。)
=050] (1) [ABD] #
=100] (2) [ABE,] [ABF,]
3} E
similar (類同上) #
=100] (4) [,AB(C|D|E|F)]
2} C+D
similar #
=090] (12) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
2}
現在問題在若第一次稱出 90 g,要分辦剩下的 12 種可能。剩下的兩次中絕不能稱 1 塊,且勢必有一次要稱 3 塊, (因為其中一次稱 1 塊 最多只有 2×4=8 種結果、兩次都稱 2 塊的話最多只有 3×3=9 種結果都不夠。),而且還要確保一次稱 3 塊的時候會有 4 種結果。
假設第二次稱 2 塊,再稱 A+B 沒有意義,所以必定是稱 (A|B)+(C|D|E|F) (如 A+C) 或 C~F 中選 2 塊 (如 C+D);分別寫下結果與可能性:
1} A+B
=080] #
=100] #
=090] (12) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
2} A+C
=080] (3) [AC(D|E|F),]
=100] (3) [BDE,] [BDF,] [BEF,]
=090] (6) ...
3}
2} C+D
=080] (2) [(A|B)CD,]
=100] (2) [(A|B)EF,]
=090] (8) ...
3}
可以看出來當第二次稱 2 塊又稱得 90 g 的時候,將還會剩下 6 種或 8 種可能性(懶得列舉,以 12 減去 80 和 100 g 時的可能性數量即是),都是無法在第三次的稱重結果(最多 4 種)中完全分辨的。
假設第二次稱 3 塊,再稱 A+B+(C|D|E|F) 相當於只稱一塊無意義;其餘不失一般性的記錄如下:
1} A+B
=080] #
=100] #
=090] (12) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
2} A+C+D
=120] (1) [ACD,] #
=150] (1) [BEF,] #
=130] (5) ...
=140] (5) ...
3}
2} C+D+E
=120] (0) (在稱第一次後的 12 種可能性中,不包含此狀況)
=150] (0)
=130] (6) ...
=140] (6) ...
3}
可以看出來當第二次稱 3 塊稱得 130 或 140 g 的時候,將至少剩下 5 種可能性(懶得列舉,用 12 減去 120 和 150 g 的可能性數量後至少還有 10 種,那麼表示 130 和 140 g 至少其中一個的可能性數目大於等於 5),都是無法在第三次的稱重結果(最多 4 種)中完全分辨的。
因此,第一次先稱 2 塊積木的話,是無解的。
所以,第一次只好先稱 3 塊積木了,假設是稱 A+B+C , 那麼 120 g 和 150 g 就分別有 1 種可能性,而 130 和 140 g 則分別有 9 種必須進一步辨別。先處理 130 g 的情形即可, 140 g 的會類似。
假設第二次只稱 1 塊積木,不失一般性,稱 A 或稱 D 。記錄如下:
1} A+B+C
=120] (1) [ABC,] #
=150] (1) [DEF,] #
=130] (9) [AB(D|E|F),] [AC(D|E|F),] [BC(D|E|F),]
2} A
=040] (6) [AB(D|E|F),] [AC(D|E|F),]
=050] (3) [BC(D|E|F),]
2} D
=040] (3) [ABD,] [ACD,] [BCD,]
=050] (6)
3}
=140] (9)
2}
可以看出來當第二次稱 1 塊的時候,至少有一種結果會剩下 6 種可能性,無法在第三次的稱重結果中完全分辨。
假設第二次稱 2 塊積木;如稱 A~C 當中的兩個則相當於只稱一個無意義,其餘記錄如下:
1} A+B+C
=120] (1) [ABC,] #
=150] (1) [DEF,] #
=130] (9) [AB(D|E|F),] [AC(D|E|F),] [BC(D|E|F),]
2} A+D
=080] (2) [ABD,] [ACD,]
=100] (2) [BC(E|F),AD]
=090] (5) [AB(E|F),] [AC(E|F)] [BCD,]
3}
2} D+E
=080] (0)
=100] (3) [ABF,] [ACF,] [BCF,]
=090] (6)
3}
=140] (9)
2}
可以看出來當第二次稱 2 塊稱得 90 g 的時候,將至少剩下 5 種可能性,無法在第三次的稱重結果中完全分辨。
那麼第二次只好也稱 3 塊積木了;如稱 A+B+C 或 D+E+F 則無意義,其餘記錄如下:
1} A+B+C
=120] (1) [ABC,] #
=150] (1) [DEF,] #
=130] (9) [AB(D|E|F),] [AC(D|E|F),] [BC(D|E|F),]
2} A+B+D
=120] (1) [ABD,] #
=150] (0)
=130] (4) [AB(E|F),] [(A|B)CD,]
=140] (4) [AC(E|F),] [BC(E|F),]
3}
2} A+D+E
=120] (0)
=150] (1) [BCF,] #
=130] (4) [AB(D|E),] [AC(D|E),]
=140] (4) [A(B|C)F,] [BC(D|E),]
3}
=140] (9)
2}
發現當第二次稱 3 塊稱得 130 或 140 g 的時候,都有 4 種可能性。因此第三次只好也稱 3 塊積木,期望有 4 種結果 (即 120, 130, 140, 150 g) 各對應 4 種可能性; 可惜這是辦不到的。
舉例來說,第二次稱 A+B+D 得到 130 g:倘若第三次稱可以有 4 種結果,故必有一種結果是 120 g 的,而根據前兩次稱等的結果,這三塊積木必為 ABE, ABF, ACD, BCD 這 4 種其中一種組合;另一方面也必有一種結果是 150 g 的,而這三塊積木必為 CDE, CDF, BEF, CEF 這 4 種其中一種組合;可以發現兩種結果並沒有共同可能的組合,也就是說,無法找到一種三塊積木的組合會同時可能稱出 120 g 和 150 g 的結果,當然也就不可能有 4 種結果以分辦剩下的 4 種可能性了。其他情況亦類似。
另外一種取巧的解釋:因為三次都是稱 3 塊,而第一次稱完後,連第二次稱都無法得到 4 種結果 (必有 120 或 150 g 的可能性數目為 0),遑論第三次呢?
所以很遺憾地,本題並無至少稱三次的解。
稱四次的解法倒是有許多種,在此提供一種:(有其它朋友在留言提出另外解法)
1} A+B+C
=120] (1) [ABC,] #
=150] (1) [DEF,] #
=130] (9) [AB(D|E|F),] [AC(D|E|F),] [BC(D|E|F),]
2} A+D
=080] (2) [ABD,] [ACD,]
3} B #
=100] (2) [BC(E|F),AD]
3} E #
=090] (5) [AB(E|F),] [AC(E|F)] [BCD,]
3} B+E
=080] (1) [ABE,] #
=100] (1) [ACF,] #
=090] (3) [ABF,] [ACE,] [BCD,]
4} A+E
=080] (1) [ACE,] #
=100] (1) [BCD,] #
=090] (1) [ABF,] #
=140] (9)
2} similar #
結論:天平比磅秤好用…
先注意到,一次稱 1 塊積木最多可得 2 種結果 (40, 50 g),2 塊積木最多可得 3 種結果 (80, 90, 100 g),3 塊積木最多可得 4 種結果 (120, 130, 140, 150 g);而因為六塊積木總重已知,稱 4 塊與稱 2 塊一樣最多只有 3 種結果,稱 5 塊和 稱 1 塊一樣。
現在令目標是最多稱三次;六塊積木分別編號 A~F。
如果第一次僅稱 1 塊積木,那麼會是無解的。因為第一次稱完後,剩下的 5 塊重量分配有 C(5,2)=10 種可能性;但是之後從這剩下的 5 塊中即使拿 3 塊來稱,最多只可得 3 種結果 (而非 4 種,因為會少掉一種三塊等重,即 120 g 或 150 g 的結果);如今僅剩兩次可稱,最多僅可得到 3×3=9 種結果,不夠分別剩下的 10 種可能性。
如果第一次稱 2 塊積木:假設稱 A+B
先介紹我記錄稱重過程的格式,之後的記錄會此依格式作簡寫,較為清楚且便利。
第 1 次} 稱 A+B
結果= 80 克] (在此結果下,積木的重量共有 4 種可能,如右) [AB(C|D|E|F),] (中括號用來列出六塊積木重量的可能性:"[,]"內逗號左邊是是 40 g ,右邊的是 50 g ;而 (C|D|E|F) 表示可能為 C,D,E,F 其中一塊。只要 40 或 50 g 有一邊寫滿三塊,另一邊亦可得知,故省略之)
結果=100 克] (在此結果下,積木的重量共有 4 種可能,如右) [,AB(C|D|E|F)]
結果= 90 克] (在此結果下,積木的重量共有 12 種可能,如右) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
接下來想第二次要怎麼稱。在這之前,以簡寫方式記錄,把第一次稱的結果記錄繼續加寫, 比較清楚:
1} A+B
=080] (4) [AB(C|D|E|F),]
2}
=100] (4) [,AB(C|D|E|F)]
2}
=090] (12) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
2}
先想第一次得出結果是 80 g 的話,第二次該怎麼稱。因為已知 A,B 了,剩下的 C~F 還有 4 種可能,而此時從 C~F 中選 2 塊稱的話,只會有 2 種結果 (90 或 100 g,而非 3 種),假設稱 C+D ,那麼可得:
1} A+B
=080] (4) [AB(C|D|E|F),]
2} C+D
=090] (2) [ABC,] [ABD,]
3}
=100] (2) [ABE,] [ABF,]
3}
=100] (4) [,AB(C|D|E|F)]
2}
=090] (12) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
2}
觀察以上,發現第二次稱得結果分別是 90 或 100 g 時,第三次分別稱 C 或 E 即可分辨所有方塊。
同理,當第一次得出結果是 100 g 的話,第二、第三次也可以類似的方法得出。記錄如下:
1} A+B
=080] (4) [AB(C|D|E|F),]
2} C+D
=090] (2) [ABC,] [ABD,]
3} C
=040] (1) [ABC] # (打井號表示六塊積木重量全都得知了。)
=050] (1) [ABD] #
=100] (2) [ABE,] [ABF,]
3} E
similar (類同上) #
=100] (4) [,AB(C|D|E|F)]
2} C+D
similar #
=090] (12) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
2}
現在問題在若第一次稱出 90 g,要分辦剩下的 12 種可能。剩下的兩次中絕不能稱 1 塊,且勢必有一次要稱 3 塊, (因為其中一次稱 1 塊 最多只有 2×4=8 種結果、兩次都稱 2 塊的話最多只有 3×3=9 種結果都不夠。),而且還要確保一次稱 3 塊的時候會有 4 種結果。
假設第二次稱 2 塊,再稱 A+B 沒有意義,所以必定是稱 (A|B)+(C|D|E|F) (如 A+C) 或 C~F 中選 2 塊 (如 C+D);分別寫下結果與可能性:
1} A+B
=080] #
=100] #
=090] (12) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
2} A+C
=080] (3) [AC(D|E|F),]
=100] (3) [BDE,] [BDF,] [BEF,]
=090] (6) ...
3}
2} C+D
=080] (2) [(A|B)CD,]
=100] (2) [(A|B)EF,]
=090] (8) ...
3}
可以看出來當第二次稱 2 塊又稱得 90 g 的時候,將還會剩下 6 種或 8 種可能性(懶得列舉,以 12 減去 80 和 100 g 時的可能性數量即是),都是無法在第三次的稱重結果(最多 4 種)中完全分辨的。
假設第二次稱 3 塊,再稱 A+B+(C|D|E|F) 相當於只稱一塊無意義;其餘不失一般性的記錄如下:
1} A+B
=080] #
=100] #
=090] (12) [(A|B)CD,] [(A|B)CE,] [(A|B)CF,] [(A|B)DE,] [(A|B)DF,] [(A|B)EF,]
2} A+C+D
=120] (1) [ACD,] #
=150] (1) [BEF,] #
=130] (5) ...
=140] (5) ...
3}
2} C+D+E
=120] (0) (在稱第一次後的 12 種可能性中,不包含此狀況)
=150] (0)
=130] (6) ...
=140] (6) ...
3}
可以看出來當第二次稱 3 塊稱得 130 或 140 g 的時候,將至少剩下 5 種可能性(懶得列舉,用 12 減去 120 和 150 g 的可能性數量後至少還有 10 種,那麼表示 130 和 140 g 至少其中一個的可能性數目大於等於 5),都是無法在第三次的稱重結果(最多 4 種)中完全分辨的。
因此,第一次先稱 2 塊積木的話,是無解的。
所以,第一次只好先稱 3 塊積木了,假設是稱 A+B+C , 那麼 120 g 和 150 g 就分別有 1 種可能性,而 130 和 140 g 則分別有 9 種必須進一步辨別。先處理 130 g 的情形即可, 140 g 的會類似。
假設第二次只稱 1 塊積木,不失一般性,稱 A 或稱 D 。記錄如下:
1} A+B+C
=120] (1) [ABC,] #
=150] (1) [DEF,] #
=130] (9) [AB(D|E|F),] [AC(D|E|F),] [BC(D|E|F),]
2} A
=040] (6) [AB(D|E|F),] [AC(D|E|F),]
=050] (3) [BC(D|E|F),]
2} D
=040] (3) [ABD,] [ACD,] [BCD,]
=050] (6)
3}
=140] (9)
2}
可以看出來當第二次稱 1 塊的時候,至少有一種結果會剩下 6 種可能性,無法在第三次的稱重結果中完全分辨。
假設第二次稱 2 塊積木;如稱 A~C 當中的兩個則相當於只稱一個無意義,其餘記錄如下:
1} A+B+C
=120] (1) [ABC,] #
=150] (1) [DEF,] #
=130] (9) [AB(D|E|F),] [AC(D|E|F),] [BC(D|E|F),]
2} A+D
=080] (2) [ABD,] [ACD,]
=100] (2) [BC(E|F),AD]
=090] (5) [AB(E|F),] [AC(E|F)] [BCD,]
3}
2} D+E
=080] (0)
=100] (3) [ABF,] [ACF,] [BCF,]
=090] (6)
3}
=140] (9)
2}
可以看出來當第二次稱 2 塊稱得 90 g 的時候,將至少剩下 5 種可能性,無法在第三次的稱重結果中完全分辨。
那麼第二次只好也稱 3 塊積木了;如稱 A+B+C 或 D+E+F 則無意義,其餘記錄如下:
1} A+B+C
=120] (1) [ABC,] #
=150] (1) [DEF,] #
=130] (9) [AB(D|E|F),] [AC(D|E|F),] [BC(D|E|F),]
2} A+B+D
=120] (1) [ABD,] #
=150] (0)
=130] (4) [AB(E|F),] [(A|B)CD,]
=140] (4) [AC(E|F),] [BC(E|F),]
3}
2} A+D+E
=120] (0)
=150] (1) [BCF,] #
=130] (4) [AB(D|E),] [AC(D|E),]
=140] (4) [A(B|C)F,] [BC(D|E),]
3}
=140] (9)
2}
發現當第二次稱 3 塊稱得 130 或 140 g 的時候,都有 4 種可能性。因此第三次只好也稱 3 塊積木,期望有 4 種結果 (即 120, 130, 140, 150 g) 各對應 4 種可能性; 可惜這是辦不到的。
舉例來說,第二次稱 A+B+D 得到 130 g:倘若第三次稱可以有 4 種結果,故必有一種結果是 120 g 的,而根據前兩次稱等的結果,這三塊積木必為 ABE, ABF, ACD, BCD 這 4 種其中一種組合;另一方面也必有一種結果是 150 g 的,而這三塊積木必為 CDE, CDF, BEF, CEF 這 4 種其中一種組合;可以發現兩種結果並沒有共同可能的組合,也就是說,無法找到一種三塊積木的組合會同時可能稱出 120 g 和 150 g 的結果,當然也就不可能有 4 種結果以分辦剩下的 4 種可能性了。其他情況亦類似。
另外一種取巧的解釋:因為三次都是稱 3 塊,而第一次稱完後,連第二次稱都無法得到 4 種結果 (必有 120 或 150 g 的可能性數目為 0),遑論第三次呢?
所以很遺憾地,本題並無至少稱三次的解。
稱四次的解法倒是有許多種,在此提供一種:(有其它朋友在留言提出另外解法)
1} A+B+C
=120] (1) [ABC,] #
=150] (1) [DEF,] #
=130] (9) [AB(D|E|F),] [AC(D|E|F),] [BC(D|E|F),]
2} A+D
=080] (2) [ABD,] [ACD,]
3} B #
=100] (2) [BC(E|F),AD]
3} E #
=090] (5) [AB(E|F),] [AC(E|F)] [BCD,]
3} B+E
=080] (1) [ABE,] #
=100] (1) [ACF,] #
=090] (3) [ABF,] [ACE,] [BCD,]
4} A+E
=080] (1) [ACE,] #
=100] (1) [BCD,] #
=090] (1) [ABF,] #
=140] (9)
2} similar #
結論:天平比磅秤好用…
8,607
上一道精選創造力謎題
下一道精選創造力謎題
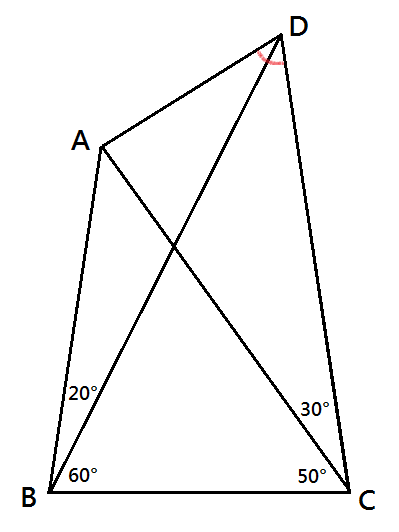 如圖,有一個四邊形 ABCD 。其中 ∠ABD = 20° ,∠CBD = 60° ,∠ACD =...
如圖,有一個四邊形 ABCD 。其中 ∠ABD = 20° ,∠CBD = 60° ,∠ACD =... 請用 三個 2 來組成算式,使其計算結果等於 1、2 、3 …、13:
例如:
6 = 2 + 2 ...
請用 三個 2 來組成算式,使其計算結果等於 1、2 、3 …、13:
例如:
6 = 2 + 2 ...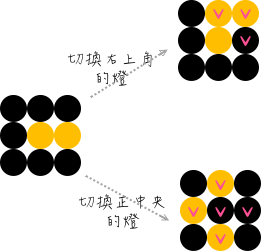 點燈遊戲是一種很常見的益智小品,規則是:
有一些燈並排在一起,每次可切換一個燈的狀態,原本是亮的就會...
點燈遊戲是一種很常見的益智小品,規則是:
有一些燈並排在一起,每次可切換一個燈的狀態,原本是亮的就會...