上一道精選數學謎題
下一道精選數學謎題
三個 2數學謎題
答對率:61%
例如:
6 = 2 + 2 + 2
8 = 2 × 2 × 2 = (2 + 2) × 2
可以使用任何計算符號或常見的函數,如:四則運算、括號、根號、小數點、平方 (會用到一個 2 ) …等等;如果願意,用三角函數也可以。但是式子中不能包含 2 以外的數字 (如:立方根符號會有一個 3 故不能用,π 算是數字 也不能用),而且要剛好用到 三個 2 ,不多不少。
那麼,該如何表示 1 ~ 13 呢?
P.S. 上面舉例過的 6 和 8 的式子就不算囉!請自行再想別的式子來表示吧~

P.S. 上面舉例過的 6 和 8 的式子就不算囉!請自行再想別的式子來表示吧~

P.S. 高斯符號 [x] 表示不大於 x 的最大整數,用這個有點犯規了,禁用!
P.S. 請使用十進位!
看答案
以下舉幾種方法:
1 = √2 × √2 ÷ 2 = 2 - 2 ÷ 2
2 = 2 + 2 - 2 = 2 × 2 ÷ 2
3 = 2 + 2 ÷ 2 = 2 + cos(2 - 2)
4 = √2 × √2 × 2 = √2 × √2 + 2
5 = 2 ÷ 2 ÷ .2 (此處 .2 是 0.2 的簡寫 用來偷懶) = [ √(2 ÷ sin(2°)) ] - 2 (此處的中括號是高斯符號,[x] 表示 不大於 x 的最大整數,用這個犯規了…以下不再用) = H(2, 2+2) (這裡的 H 是重覆組合符號)
6 = 2 × 2 + 2 = 22 + 2 = C(2+2, 2) (這裡的 C 是組合符號)
7 = 2 ÷ .2 - 2 (此處 .2 是指 0.2222... = 2/9,2 為循環節,本來那一槓要寫在 2 的上面的,但目前沒有加頂線的功能。)
8 = 22 × 2 = 2 ^ H(2, 2) (^ 在此為次方符號,例:3^2 = 32 = 9)
9 = √2 × √2 ÷ .2 = H(2, 2) ^ 2
10 = √2 × √2 ÷ .2
11 = 22 ÷ 2 = 2 ÷ .2 + 2
12 = 2 ÷ .2 + 2 = (2+2)! ÷ 2 (! 在此為階乘符號)
13 = 2 × 2 × 2 於五進位時… (這算是犯規了)
其實,13 以上的正整數,要湊出來都有點難 (除了特定幾個數字和用較不常見的函數之外)…。以下提供一種可以算出任何正整數的解法:
使用對數的話就能做到!簡單介紹一下,對數 (符號是 log) 的意義是:
如果 z = logx y ,就表示「y 是 x 的 z 次方」,也就是 xz= y ;例如: 23= 8 ,則 log2 8 = 3。
本題的通解:對於任何正整數 n
n = - log2 (log2 (√√√…√2) ) (共開 n 次根號)
原因在於,根號 2 表示 2 的 1/2 次方;把 2 開了 n 次根號,就表示 2 的 (1/2)n次方。故 log2 (√√√…√2) = log2 (2 ^ (1/2)n) = (1/2)n= 2-n
故 - log2 (log2 (√√√…√2) ) = - log2 (2-n) = - (-n) = n
用這個通式的話,就可以用三個 2 表示任何正整數。
例如:5 = - log2 (log2 (√√√√√2) )
「有的函數沒學過嗎?」以下補充解答與留言當中用到的函數的意義,讓大家都盡量都看得懂:)
1 = √2 × √2 ÷ 2 = 2 - 2 ÷ 2
2 = 2 + 2 - 2 = 2 × 2 ÷ 2
3 = 2 + 2 ÷ 2 = 2 + cos(2 - 2)
4 = √2 × √2 × 2 = √2 × √2 + 2
5 = 2 ÷ 2 ÷ .2 (此處 .2 是 0.2 的簡寫 用來偷懶) = [ √(2 ÷ sin(2°)) ] - 2 (此處的中括號是高斯符號,[x] 表示 不大於 x 的最大整數,用這個犯規了…以下不再用) = H(2, 2+2) (這裡的 H 是重覆組合符號)
6 = 2 × 2 + 2 = 22 + 2 = C(2+2, 2) (這裡的 C 是組合符號)
7 = 2 ÷ .
8 = 22 × 2 = 2 ^ H(2, 2) (^ 在此為次方符號,例:3^2 = 32 = 9)
9 = √2 × √2 ÷ .
10 = √2 × √2 ÷ .2
11 = 22 ÷ 2 = 2 ÷ .
12 = 2 ÷ .2 + 2 = (2+2)! ÷ 2 (! 在此為階乘符號)
13 = 2 × 2 × 2 於五進位時… (這算是犯規了)
其實,13 以上的正整數,要湊出來都有點難 (除了特定幾個數字和用較不常見的函數之外)…。以下提供一種可以算出任何正整數的解法:
使用對數的話就能做到!簡單介紹一下,對數 (符號是 log) 的意義是:
如果 z = logx y ,就表示「y 是 x 的 z 次方」,也就是 xz= y ;例如: 23= 8 ,則 log2 8 = 3。
本題的通解:對於任何正整數 n
n = - log2 (log2 (√√√…√2) ) (共開 n 次根號)
原因在於,根號 2 表示 2 的 1/2 次方;把 2 開了 n 次根號,就表示 2 的 (1/2)n次方。故 log2 (√√√…√2) = log2 (2 ^ (1/2)n) = (1/2)n= 2-n
故 - log2 (log2 (√√√…√2) ) = - log2 (2-n) = - (-n) = n
用這個通式的話,就可以用三個 2 表示任何正整數。
例如:5 = - log2 (log2 (√√√√√2) )
「有的函數沒學過嗎?」以下補充解答與留言當中用到的函數的意義,讓大家都盡量都看得懂:)
- 階乘 n! (n 要是正整數或 0):從 n 開始乘 (n-1)、乘 (n-2)、…直到 1 為止,如 5! = 5 × 4 × 3 × 2 × 1 = 120 ;0! = 1 (當作定義)
- 組合 C(m, n) (m, n 要是正整數或 0 ,m ≥ n):從 m 個相異物中取出 n 個來的方法數 (不包含順序),如 C(3, 2) = 3 因為從三個東西 (ABC) 中選二,方法有 AB、AC、BC 三種。公式是 C(m, n) = m! / n! / (m-n)!
- 排列 P(m, n) (m, n 要是正整數或 0 ,m ≥ n):從 m 個相異物中取出 n 個來之後排列,其排列方法數 (有包含順序)。如 P(3, 2) = 6 因為從三個東西 (ABC) 中選二再排列,方法有 AB、BA、AC、CA、BC、CB 六種。公式是 P(m, n) = m! / (m-n)!
- 重覆組合 H(m, n) (m, n 要是正整數或 0):把 n 個相同的東西分給 m 個相異的人,其分配的方法數。如 H(2, 3) = 4 ,因為把 3 個相同的球,分給兩人(甲乙),分法有:甲 0 個乙 3 個、甲 1 個乙 2 個、甲 2 個乙 1 個、甲 3 個乙 0 個,共 4 種。公式為:H(m, n) = (m+n-1)! / n! / (m-1)!
- 三角函數們 sin、cos、tan:在此解釋較難。高一數學會教,有興趣 google 吧…
- 指數(次方)、根號與對數:上面有介紹了,用一個例子總結他們之間的關係:
23 = 8 所以: 3√8 = 8 ^ (1/3) = 2 ;log2 8 = 3 - 平方根 √x 又可寫作 sqrt(x)。
- 最大值 / 最小值 max() / min () :取出一群數 (可任意多個,寫在括號中) 中最大的/最小的。如 max(3, 5) = 5 取最大的; min (1, -1, 3) = -1 取最小的。
- 費氏數 fib(n) (n 是正整數或 0):給出費氏數列 (0, 1, 1, 2, 3, 5, 8, ...) 中的第 n 個數,最前面的 0 算是第零個。故: fib(0) = 0, fib(1) = 1, fib(2) = fib(1) + fib(0) = 1, fib(3) = fib(2) + fib(1) = 2 ,第二個以後的費氏數都是前兩個相加,以此類推。
- 質數 prime(n) (n 是正整數):給出由小到大的第 n 個質數 (2, 3, 5, 7, 11, ...),如 prime(1) = 2 、prime(2) = 3 、prime(6) = 13。
- 餘數 mod(m, n) 或是寫 m (mod n) (m 要是整數、 n 要是正整數):給出 m 除以 n 的餘數。如 mod(17, 3) = 2; 8 (mod 3) = 2 (mod 3) = -1 (mod 3)。
- 最大公因數 gcd() 和最小公倍數 lcm() (括號內要放正整數,個數不限)。例:gcd(16, 24) = 8, lcm(4, 5, 6) = 60。
7,877
上一道精選數學謎題
下一道精選數學謎題
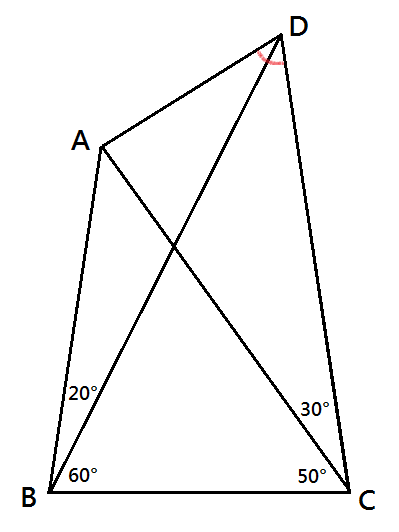 如圖,有一個四邊形 ABCD 。其中 ∠ABD = 20° ,∠CBD = 60° ,∠ACD =...
如圖,有一個四邊形 ABCD 。其中 ∠ABD = 20° ,∠CBD = 60° ,∠ACD =... 日期的表示在各個國家有不同的習慣寫法,
比如說1月3日,有些國家習慣寫1.3,有些習慣寫3.1,
常...
日期的表示在各個國家有不同的習慣寫法,
比如說1月3日,有些國家習慣寫1.3,有些習慣寫3.1,
常... 有一個密封的瓶子,裡面裝了600 c.c.的果汁,但並沒有裝滿(如下圖);
你手邊只有一把直尺,請問...
有一個密封的瓶子,裡面裝了600 c.c.的果汁,但並沒有裝滿(如下圖);
你手邊只有一把直尺,請問... 地球是不斷在自轉中的。
一般人用力往上跳,一瞬間就會掉下來,
掉回地面的時候還是在原地;
那如果是鋼...
地球是不斷在自轉中的。
一般人用力往上跳,一瞬間就會掉下來,
掉回地面的時候還是在原地;
那如果是鋼...