上一道數學謎題
下一道數學謎題
三個圓數學謎題
答對率:77%
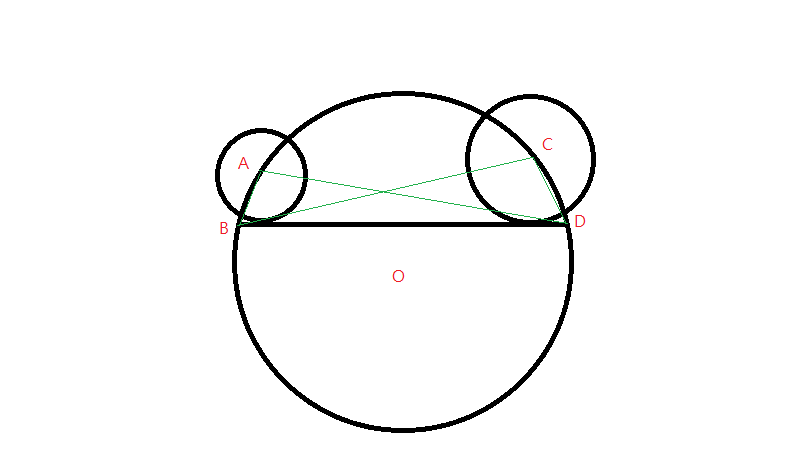
有三個人站立在同一塊地上的三個不同點,分別是A.C.O
如果用這三的點,半徑未知畫三個圓,其中讓A和C在圓O上
發現如果在圓O上取一條弦BD,會剛好跟圓A和圓C相切
經測量得AB=2 AD=9 BC=8 CD=4
那請問所取的圓A半徑和圓C半徑的比是多少?
看答案
9:16
解析
我要編輯從A和C做垂直交BD於E和F
AE:CF即為題目所求
△ABD : △BCD
=1/2xABxADx(sin ∠BAD):1/2xBCxCDx(sin ∠BCD)
=1/2x2x9x(sin ∠BAD):1/2x4x8x(sin ∠BAD) ( ∠BAD和∠BCD對等弧故相等)
=9:16
但△ABD : △BCD又可表為
1/2xBDxAE:1/2xBDxCF
=AE:CF
故AE:CF=9:16
還不會三角函數(sin) 的朋友,可以用以下方法算 △ACD : △BCD 三角形面積比:
因為 ∠BAD = ∠BCD (等弧圓周角) ,所以把這兩個三角形拿出來,讓這個角重疊,如下圖。
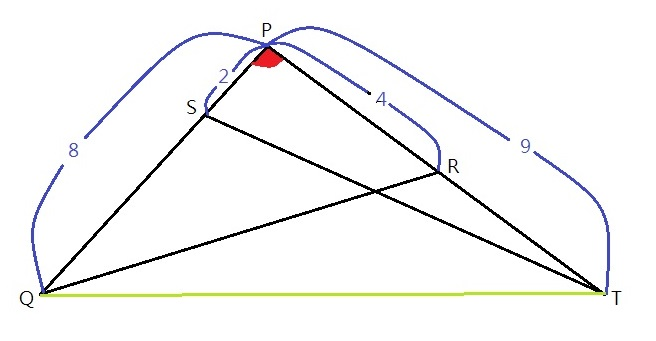
等角的頂點改叫 P ,兩個三角形分別為 △PQR 和 △PST。現在,連接 QT。
可看出 △PST : △PQT = 2 : 8 = 1 : 4 (共頂點Q 故高相同,所以 面積比 = 底邊比)
故△PST=1/4△PST
同理, △PQR : △PQT = 4 : 9
△PQR=4/9△PQT
因此, △ABD : △BCD = △PST : △PQR = 1/4 :9/4 = 9 : 16=半徑比
AE:CF即為題目所求
△ABD : △BCD
=1/2xABxADx(sin ∠BAD):1/2xBCxCDx(sin ∠BCD)
=1/2x2x9x(sin ∠BAD):1/2x4x8x(sin ∠BAD) ( ∠BAD和∠BCD對等弧故相等)
=9:16
但△ABD : △BCD又可表為
1/2xBDxAE:1/2xBDxCF
=AE:CF
故AE:CF=9:16
還不會三角函數(sin) 的朋友,可以用以下方法算 △ACD : △BCD 三角形面積比:
因為 ∠BAD = ∠BCD (等弧圓周角) ,所以把這兩個三角形拿出來,讓這個角重疊,如下圖。

等角的頂點改叫 P ,兩個三角形分別為 △PQR 和 △PST。現在,連接 QT。
可看出 △PST : △PQT = 2 : 8 = 1 : 4 (共頂點Q 故高相同,所以 面積比 = 底邊比)
故△PST=1/4△PST
同理, △PQR : △PQT = 4 : 9
△PQR=4/9△PQT
因此, △ABD : △BCD = △PST : △PQR = 1/4 :9/4 = 9 : 16=半徑比
5,101
上一道數學謎題
下一道數學謎題
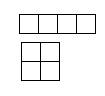 我又回來玩磁磚了喔~
本次所使用的磁磚是:
這兩種。其中長條型有15個,正方形有1個
欲拼滿8x8格...
我又回來玩磁磚了喔~
本次所使用的磁磚是:
這兩種。其中長條型有15個,正方形有1個
欲拼滿8x8格...