上一道精選數學謎題
下一道精選數學謎題
公平的協議 2數學謎題
答對率:63%
四人輪流拿金幣,一人每次拿 2 個;若剛好分完則沒問題;有若剩餘的金幣的話,就會是 1~7 個。因為每種剩餘的狀況均等(都是 1/8),故這樣分:
剩 1 個或剩 6 個時,給海盜 A;
剩 2 個或剩 5 個時,給海盜 B;
剩 3 個或剩 4 個時,給海盜 C;
剩 7 個時,給海盜 D。
這樣,每個人多得的金幣的期望值都是 7/8 個,看來很公平。
不過這時候,有人說話了:
「嘿~等等,這不公平!」D 說。
「有什麼好不公平的,大家多得金幣的期望值都是 7/8 個啊。」B 說。
「但是我只有 1/8 的機率能多得金幣,除了剛好分完的情況,另外 6/8 (3/4) 的機率是連一個多的金幣都分不到啊;而像 C ,他有 2/8 (1/4) 的機率能多得 3 個金幣以上!」D 忿忿不平的抱怨著。
「你雖然多得金幣的機率只有 1/8,但若你運氣好,一次就多拿 7 個金幣。高報酬就有高風險嘛,你這樣計較是不敢賭大的啊?膽小鬼,虧你還幹海盜這麼久了。」A 說。
「我就是覺得不公平嘛!如果你們都覺得公平的話,不然 C 你跟我換應該也 OK 啊;金幣剩 7 個的時候都歸你,剩 3 個或 4 個的時候歸我。」
「才~不~要~♥
 」
」然後海盜們又開始為分金幣爭論不休了…。
那麼,有什麼公平的金幣分法,可以解決他們的問題呢?

看答案
有多種分法,此舉兩種:
(一)
這樣分的話,每人都有 3 種情況可以多得 1 個金幣、2 種情況可以多得 2 個金幣 (7 = 1×3 + 2×2),對四位海盜來說就都是公平的。
(二)
這樣分的話,每人都有 1 種情況可以多得 1 個金幣、1 種情況可以多得 2 個金幣 、1 種情況可以多得 4 個金幣(7 = 1 + 2 + 4),對四位海盜來說就也都是公平的。
比較一下,第一種分法每人有 3/8 的機率可多得 1 個金幣、 2/8 的機率可多得 2 個;而第二種分法則是各有 1/8 的率可多得 1 個、2 個和 4 個,至少拿到 1 個和 2 個金幣的機會少了點,故看來風險較大。
不過至少這兩種分法,對四位海盜都是公平一致的,就看他們要願意承擔多少風險,選擇哪種分法了。
(一)
| 剩餘金幣數 | 給誰 |
| 1 | A |
| 2 | B C |
| 3 | AA D |
| 4 | A B C D |
| 5 | A B C DD |
| 6 | BB CC DD |
| 7 | AA BB CC D |
這樣分的話,每人都有 3 種情況可以多得 1 個金幣、2 種情況可以多得 2 個金幣 (7 = 1×3 + 2×2),對四位海盜來說就都是公平的。
(二)
| 剩餘金幣數 | 給誰 |
| 1 | A |
| 2 | AA |
| 3 | BB C |
| 4 | AAAA |
| 5 | BBBB D |
| 6 | CCCC DD |
| 7 | B CC DDDD |
這樣分的話,每人都有 1 種情況可以多得 1 個金幣、1 種情況可以多得 2 個金幣 、1 種情況可以多得 4 個金幣(7 = 1 + 2 + 4),對四位海盜來說就也都是公平的。
比較一下,第一種分法每人有 3/8 的機率可多得 1 個金幣、 2/8 的機率可多得 2 個;而第二種分法則是各有 1/8 的率可多得 1 個、2 個和 4 個,至少拿到 1 個和 2 個金幣的機會少了點,故看來風險較大。
不過至少這兩種分法,對四位海盜都是公平一致的,就看他們要願意承擔多少風險,選擇哪種分法了。
10,696
上一道精選數學謎題
下一道精選數學謎題
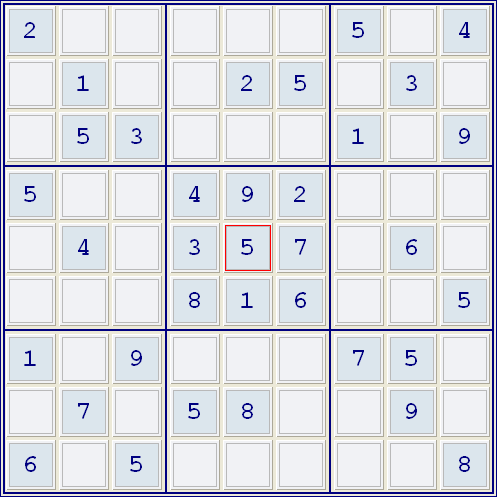 數獨遊戲中,一開始給的數字越多,就會越容易解嗎?試試看以下的題目吧。
請完成以下數獨:
解出的朋友,...
數獨遊戲中,一開始給的數字越多,就會越容易解嗎?試試看以下的題目吧。
請完成以下數獨:
解出的朋友,... 下面方框裡有一些彩色方塊,
請畫線把兩兩相同的顏色連在一起,
而且畫出來的線互相不能有相交,也不能超...
下面方框裡有一些彩色方塊,
請畫線把兩兩相同的顏色連在一起,
而且畫出來的線互相不能有相交,也不能超...