上一道精選數學謎題
下一道精選數學謎題
學習數學的歷程數學謎題
答對率:89%
但你有沒有發現,小學學的數學,到國高中好像都不記得學了什麼?
如果你還留有小學的數學課本,試著翻開回憶看看,當初學的數學常常也有一些小學生的創造力所做出的意想不到的解法。
小學的題目都給學生自由地發揮,到了國中開始出現許多限制,使得國中生的思考模式偏向機械化,而高中生則因為學到了更多工具,像是三角函數、微積分,導致時常想要砸大絕來做一些簡單的題目,有點殺雞用牛刀的感覺。
下面這個題目,小學生和國中生,還有高中生都有不同的作法
或許有人是真的看這題從小學看到高中了吧!
那麼,如果你還沒看過這題,你會怎麼做呢?
題目:
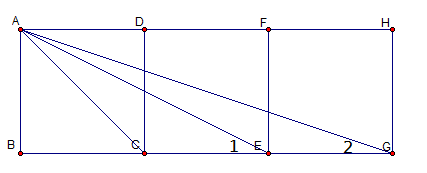
如圖,ABCD、CDFE、EFHG為三個正方形,
連接AC、AE、AG
求∠1+∠2是幾度。
看答案
45∘
此題解法頗多,歡迎分享
此題解法頗多,歡迎分享
解析
我要編輯作者:ms0592138(小分/阿分/繽紛) | 歷史版本
<<小學生的做法>>
(當然小學還沒有學正規的幾何證明,不過這裡我還是寫的正式一點)
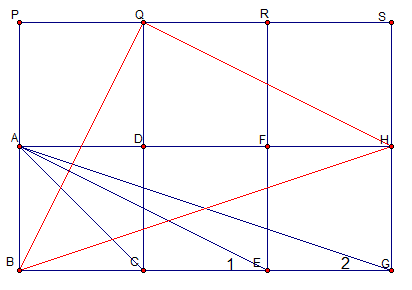
向上再多畫3個正方形PQDA、QRFD、RSHF
連QB、QH、BH,顯然:
∠1=∠QHD
∠2=∠AHB
故∠1+∠2=∠QHB
又△QHB為等腰直角三角形,故所求=45∘
<<國中生的做法>>
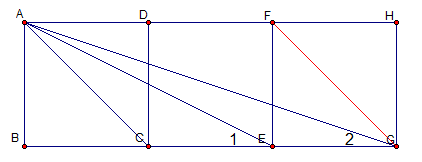
連接FG,令正方形邊長為1
在△ACE中:
AC=√2;CE=1;AE=√5
在△AFG中:
AF=2;FG=√2;AG=√10
故AC/AF=CE/FG=AE/AG=1/√2
得△ACE~△AFG(SSS相似)
所以∠1+∠2=∠AGF+∠2=∠BGF=45∘
<<高中生的做法>>
sin(∠1+∠2)
=(sin∠1)*(cos∠2)+(sin∠2)*(cos∠1)
=(1/√5)*(3/√10)+(1/√10)*(2/√5)
=1/√2=√2/2
故∠1+∠2=arcsin√2/2=45∘
==
三種解法都能解得正確解答,但你是否覺得,小學生的解法最漂亮呢?
確實我們國、高中所學的知識比小學來得深
但是往往我們的思想也在無形之中被僵化
因此有時會不管看到什麼題目,就用自己所知的一切公式、技巧來解
但是常常會浪費許多時間,還得不到正確解答
因此,當你用高等數學解不出來的時候,不妨試試用最簡單的角度切入著手
搞不好會得到意想不到的效果唷˙˙
(當然小學還沒有學正規的幾何證明,不過這裡我還是寫的正式一點)

向上再多畫3個正方形PQDA、QRFD、RSHF
連QB、QH、BH,顯然:
∠1=∠QHD
∠2=∠AHB
故∠1+∠2=∠QHB
又△QHB為等腰直角三角形,故所求=45∘
<<國中生的做法>>

連接FG,令正方形邊長為1
在△ACE中:
AC=√2;CE=1;AE=√5
在△AFG中:
AF=2;FG=√2;AG=√10
故AC/AF=CE/FG=AE/AG=1/√2
得△ACE~△AFG(SSS相似)
所以∠1+∠2=∠AGF+∠2=∠BGF=45∘
<<高中生的做法>>
sin(∠1+∠2)
=(sin∠1)*(cos∠2)+(sin∠2)*(cos∠1)
=(1/√5)*(3/√10)+(1/√10)*(2/√5)
=1/√2=√2/2
故∠1+∠2=arcsin√2/2=45∘
==
三種解法都能解得正確解答,但你是否覺得,小學生的解法最漂亮呢?
確實我們國、高中所學的知識比小學來得深
但是往往我們的思想也在無形之中被僵化
因此有時會不管看到什麼題目,就用自己所知的一切公式、技巧來解
但是常常會浪費許多時間,還得不到正確解答
因此,當你用高等數學解不出來的時候,不妨試試用最簡單的角度切入著手
搞不好會得到意想不到的效果唷˙˙
7,838
上一道精選數學謎題
下一道精選數學謎題
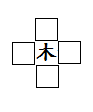 請利用空格搭配中央的字,組合成新的字
例如:
可組:呆、沐、杉、森
試著找出下面這些空格可填的字吧!...
請利用空格搭配中央的字,組合成新的字
例如:
可組:呆、沐、杉、森
試著找出下面這些空格可填的字吧!...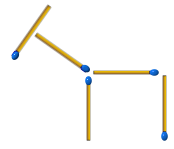 下圖是一隻用火柴簡單拼成的馬,
想讓這隻馬保持同樣的形狀,但頭朝不同方向,
你最少移動幾根火柴就可以...
下圖是一隻用火柴簡單拼成的馬,
想讓這隻馬保持同樣的形狀,但頭朝不同方向,
你最少移動幾根火柴就可以...