上一道數學謎題
下一道數學謎題
9個數字填空數學謎題
答對率:75%
使得3列分別得到1組3位數
要求:第2列的三位數要是第1列的2倍,第3列的三位數要是第1列的3倍
(答案不只一個!)
(註:此題的列、行、排都是指橫排<打解析打到一半發現三個字我都用了= =>)
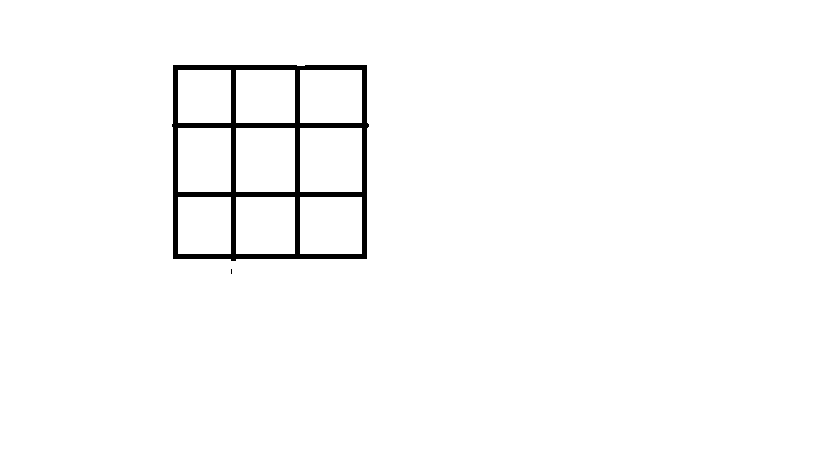
看答案
(1)
3 2 7
6 5 4
9 8 1
(2)
2 1 9
4 3 8
6 5 7
(3)
2 7 3
5 4 6
8 1 9
(4)
1 9 2
3 8 4
5 7 6
3 2 7
6 5 4
9 8 1
(2)
2 1 9
4 3 8
6 5 7
(3)
2 7 3
5 4 6
8 1 9
(4)
1 9 2
3 8 4
5 7 6
解析
我要編輯作者:ms0592138(小分/阿分/繽紛) | 歷史版本
1.先看最左上角那格
由於第三排要乘以3,所以此格不能超過3
也就是只能是1.2或3
2.看最右邊的直排
由於是個位數,不可能發生進位(有其他數字加進來)
因此可以列出可能性有:
(1,2,3)
(2,4,6)
(3,6,9)
(4,8,2)
(5,0,5)(不合)
(6,2,8)
(7,4,1)
(8,6,4)
(9,8,7)
其中(1,2,3)填入後造成左上角沒得填,因此去除
(這些等等要用)
3.從左上角開始討論
(1)左上角填3
如果百位數是3,那十位數乘以3後不得進位(不然第3列就爆了)
所以左邊那行必定是3,6,9,第1排的十位數不能超過4
那第1排的十位數就只能是1或2了
接著把我們在第2步寫出的各種組合拿出來看,把有3.6.9的都踢掉,
剩下的有(4,8,2)(7,4,1)
如果最右排寫(4,8,2)
剩下的1、5、7會發現怎樣都填不進去
如果最右排寫(7,4,1)
剩下2、5、8
剛好就可以填出來了:
3 2 7
6 5 4
9 8 1---(得到第一組解)
(2)左上角寫2
此時又分成:a.沒有任何一行進位至百位、b.第2行沒有進位第3行有、c.第2、3行都有進位
a.都沒有進位,那左邊那排就是2,4,6了
可是這麼做的話會發現,在第2步整理出的組合只剩下(9,8,7)
再把剩下的1、3、5填入,得到
2 1 9
4 3 8
6 5 7---(得到第二組解)
b.只有第3行進位,代表第一行的十位數x2<10,x3>10,可能的就是4了
但因第二行不進位,百位數一定是2x2=4,出現兩個4,不合
c.都進位,那第一行的十位數>5
因為任何數x2進位不可能進超過1(因為9x2也才18)
所以第二行百位數應是2x2+1=5
那接下來又分:甲、第三行進1;乙、第三行進2
甲、第三行進1,那百位數就是3x2+1=7
=>第一行的十位數<7,但又要>5,所以只能填6
再把第2步的組合中含有2.5.6.7的去除
發現什麼都沒有了,因此不合
乙、第三排進2,那百位數是3x2+1=8
=>第一行的十位數>6
然後照樣把第2步的組合中,含有2.5.8的去除
剩下(3,6,9)和(7,4,1)
如果最右邊填(3,6,9)
中間就填7、4、1
得:
2 7 3
5 4 6
8 1 9----(得到第三組解)
(3)左上角填1
同樣再次進行:a.沒有任何一行進位至百位、b.第2行沒有進位第3行有、c.第2、3行都有進位
a.沒有進位的話,百位數就是1、2、3了
由於不進位,第一列的十位數<4,但1~3都用掉了,因此不合
b.第2行沒有進位第3行有
所以第一列的十位數<5且>3,那就是4
把第2步的組合刪掉又1.2.3.4的,剩下(9,8,7)
填入9、8、7,由於第三排在各位數進了2,所以十位數是4x3+2的末位,還是4,因此不合
c.都進位
=>第二列百位數=1x2+1=3
那再分甲、第三列進1;乙、第三列進2
甲:第三列只進1,那第一列的十位數=6,第三行百位數=1x3+1=4
把第2步的組合含有1.3.4.6的刪除
又只剩(9,8,7)
第三行的十位數=6x3+2=20(不合)
乙:第三排進2,那第三排的百位數應是1x3+2=5,且第一排的十位數>6
把第2步組合中含有1.3.5的去掉
剩下的有(2,4,6)(4,8,2)(6,2,8)(8,6,4)(9,8,7)
由於且第一排的十位數一定是7~9,所以(9,8,7)不合
填入(2,4,6),剩下的恰可填入(9,8,7)
填入(4,8,2)剩下6、7、9,任何一個填入第一排十位數,都會發現乘以2後的個位數已經用掉,不合
剩下的依此類推。
因此得到第四組解:
1 9 2
3 8 4
5 7 6
註:或許有人發現其中的解可以由分組對換得到,但避免遺漏其他不適用對換的解,在此還是貼詳細證明。
由於第三排要乘以3,所以此格不能超過3
也就是只能是1.2或3
2.看最右邊的直排
由於是個位數,不可能發生進位(有其他數字加進來)
因此可以列出可能性有:
(2,4,6)
(3,6,9)
(4,8,2)
(5,0,5)(不合)
(6,2,8)
(7,4,1)
(8,6,4)
(9,8,7)
其中(1,2,3)填入後造成左上角沒得填,因此去除
(這些等等要用)
3.從左上角開始討論
(1)左上角填3
如果百位數是3,那十位數乘以3後不得進位(不然第3列就爆了)
所以左邊那行必定是3,6,9,第1排的十位數不能超過4
那第1排的十位數就只能是1或2了
接著把我們在第2步寫出的各種組合拿出來看,把有3.6.9的都踢掉,
剩下的有(4,8,2)(7,4,1)
如果最右排寫(4,8,2)
剩下的1、5、7會發現怎樣都填不進去
如果最右排寫(7,4,1)
剩下2、5、8
剛好就可以填出來了:
3 2 7
6 5 4
9 8 1---(得到第一組解)
(2)左上角寫2
此時又分成:a.沒有任何一行進位至百位、b.第2行沒有進位第3行有、c.第2、3行都有進位
a.都沒有進位,那左邊那排就是2,4,6了
可是這麼做的話會發現,在第2步整理出的組合只剩下(9,8,7)
再把剩下的1、3、5填入,得到
2 1 9
4 3 8
6 5 7---(得到第二組解)
b.只有第3行進位,代表第一行的十位數x2<10,x3>10,可能的就是4了
但因第二行不進位,百位數一定是2x2=4,出現兩個4,不合
c.都進位,那第一行的十位數>5
因為任何數x2進位不可能進超過1(因為9x2也才18)
所以第二行百位數應是2x2+1=5
那接下來又分:甲、第三行進1;乙、第三行進2
甲、第三行進1,那百位數就是3x2+1=7
=>第一行的十位數<7,但又要>5,所以只能填6
再把第2步的組合中含有2.5.6.7的去除
發現什麼都沒有了,因此不合
乙、第三排進2,那百位數是3x2+1=8
=>第一行的十位數>6
然後照樣把第2步的組合中,含有2.5.8的去除
剩下(3,6,9)和(7,4,1)
如果最右邊填(3,6,9)
中間就填7、4、1
得:
2 7 3
5 4 6
8 1 9----(得到第三組解)
(3)左上角填1
同樣再次進行:a.沒有任何一行進位至百位、b.第2行沒有進位第3行有、c.第2、3行都有進位
a.沒有進位的話,百位數就是1、2、3了
由於不進位,第一列的十位數<4,但1~3都用掉了,因此不合
b.第2行沒有進位第3行有
所以第一列的十位數<5且>3,那就是4
把第2步的組合刪掉又1.2.3.4的,剩下(9,8,7)
填入9、8、7,由於第三排在各位數進了2,所以十位數是4x3+2的末位,還是4,因此不合
c.都進位
=>第二列百位數=1x2+1=3
那再分甲、第三列進1;乙、第三列進2
甲:第三列只進1,那第一列的十位數=6,第三行百位數=1x3+1=4
把第2步的組合含有1.3.4.6的刪除
又只剩(9,8,7)
第三行的十位數=6x3+2=20(不合)
乙:第三排進2,那第三排的百位數應是1x3+2=5,且第一排的十位數>6
把第2步組合中含有1.3.5的去掉
剩下的有(2,4,6)(4,8,2)(6,2,8)(8,6,4)(9,8,7)
由於且第一排的十位數一定是7~9,所以(9,8,7)不合
填入(2,4,6),剩下的恰可填入(9,8,7)
填入(4,8,2)剩下6、7、9,任何一個填入第一排十位數,都會發現乘以2後的個位數已經用掉,不合
剩下的依此類推。
因此得到第四組解:
1 9 2
3 8 4
5 7 6
註:或許有人發現其中的解可以由分組對換得到,但避免遺漏其他不適用對換的解,在此還是貼詳細證明。
19,267
上一道數學謎題
下一道數學謎題