上一道精選數學謎題
下一道精選數學謎題
次方數學謎題
答對率:75%
1) 如果 x = 1,則 y 是多少?
2) 如果 x = 2 ,則 y 又是多少?
3) 如果 y = 2 ,則 x 是多少?
4) 如果 y = 3 ,則 x 又是多少?
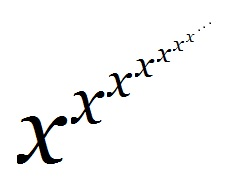 註:注意這種連續次方,要從最上層的次方開始計算,一層次方算出的值作為下面一層的指數;也就是如上述 y 的式子中的括號所示。例如:21^3 = 21 = 2 , 而不是 = (21)3 = 8 。
註:注意這種連續次方,要從最上層的次方開始計算,一層次方算出的值作為下面一層的指數;也就是如上述 y 的式子中的括號所示。例如:21^3 = 21 = 2 , 而不是 = (21)3 = 8 。P.S. 以下內容是給 有算出第三題和第四題的朋友~
再來一題:
5) 如果 y = 4 ,則 x 又是多少?跟第三題的算出來的結果比較一下吧 ~
看答案
1) 1
2) 無限大
3) √2
4) 無解
5) 無解
第一題,不管把 y 算到哪 1 層次方,都是 1 的 1 次方,所以答案還是 1 。
第二題,多算幾層次方就會發現,數字越來越大,而且增大的很快。如:22 = 4 ,24 = 16,216 = 65536,265536 = ……。可以大膽地說是無限大了。
(要證明的話,簡單來說,可以說明每算一層次方,數字至少變成原來的兩倍以上。既然 每次兩倍: 2, 4, 8, 16, ... 最後都會變成無限大,那 y = 2^(2^(2^(...^2))) 當然也是無限大。)
第三題,可用以下方法算出 x:
根據題目, y = x^(x^(x^(x^(...^x)))) ,但是因為有無限個 x 次方,所以:
y = x^(x^(x^(x^(...^x)))) = x^(x^(x^(x^(x^(...^x))))) = x^y = xy
這裡 y = 2 ,故得到 2 = x2 ,所以 x = √2 。 (注意 x 要是正實數)
第四題,如法炮製以上的方法,可得 3 = x3 ,故 x = 3√3 ≒ 1.442 。(3 的立方根)
可惜,這是錯誤的答案。如果真的把 x 代 3√3 去計算 x^(x^(x^(x^(...^x)))) ,多算幾個次方之後,會發現 x^(x^(x^(x^(...^x)))) 的值會趨近 約 2.478 (每多算一層次方,值會越來越大,但是會越來越接近 2.478... 不會再更大。),而不會是 3。
同理,第五題用以上方法得到 x = 4√4 = √2 。但是第三題已經告訴我們, x = √2 時 y 應該要是 2 (而不是 4)。
也可以用另一個看法看出第四、五題算出答案有問題。如果這兩題的解真的就是 3√3 和 4√4 = √2 的話,表示:
3√3^(3√3^…^(3√3)) = 3
√2^(√2^…^(√2)) = 4 ,大於上一行的 3 。
但是,很明顯當 x 越大的時候,y = x^(x^(x^(x^(...^x)))) 也要越大才對,而 3√3 > √2 !表示解一定有哪裡出錯了。
可以見得,看上去類似的問題,貿然用同一招來解的話,常會有誤。
以下說明,給有興趣的朋友參考:
從第三題的做法,可以知道,如果 y 存在 (歷經無限個次方之後仍是有限值,沒有發散),則 y = xy ,也就是 x = y1/y = y√y 。
畫一個 y√y 對 y 的圖:
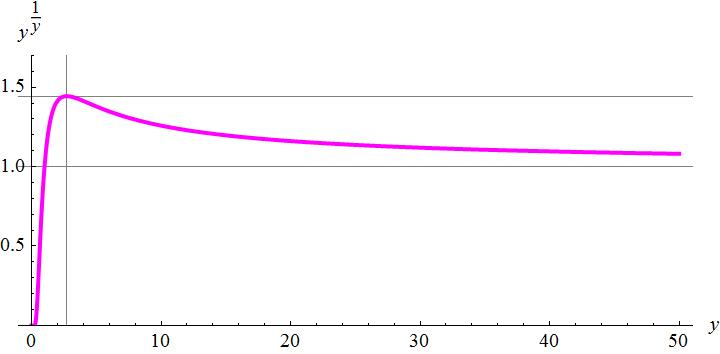
這個圖形長得很奇怪,主要的特徵如下:
把圖放大來看:
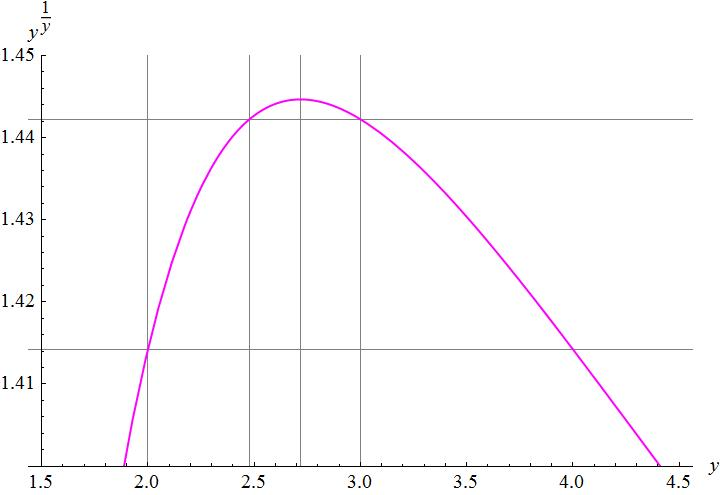
可以從圖形中看到,當 x = y√y = √2 ≒ 1.414 的時候,y = 2 是一個解 (當然,圖中還看得到右邊有另一個解是 y = 4)。這就符合第三題 (和第五題) 的情形。
第四題的情形,當 x = y√y = 3√3 ≒ 1.442 的時候,y = 3 是一個解 (較大),而 y = 2.478 也是一個解 (較小)。到底哪一個才是對的呢?如上所述實際去計算,得到 y = 2.478 才對,而不是 3 。
如果多試幾種 x, y 值,可以發現,滿足 y = x^(x^(x^(x^(...^x)))) 的 y 值,在圖中總是較小的那個解 (y < e) ,而不會是較大的解 (y > e) 。
如果會疊代法的話,可以看出這一點。例如:x = √2 ,則令函數 f(z) = (√2)z ,一開始 z 代 √2 ,算函數值,然後再代入函數 (其實這就是在一層一層地算次方),重複多次後,就會趨近 y = x^(x^(x^(x^(...^x)))) 。從圖形在看的話,如下圖:
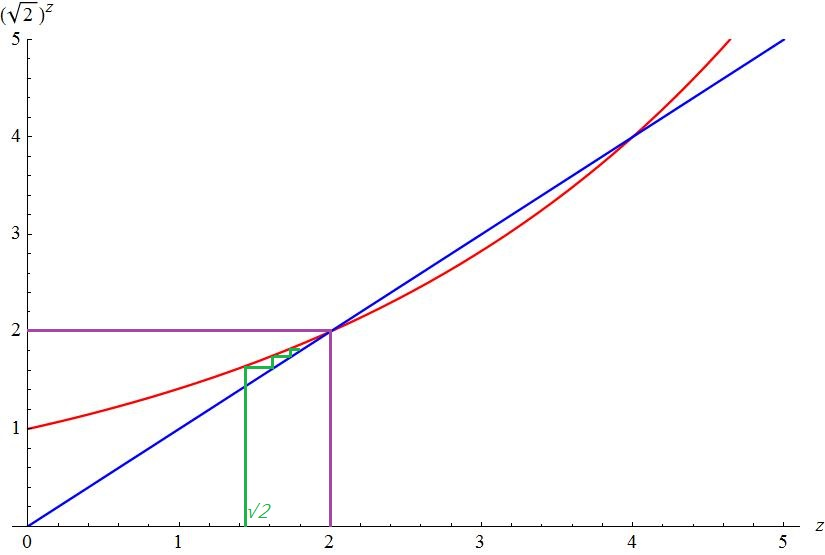
圖中,紅色曲線是 f(z) = (√2)z 的圖形,而藍色直線是 f(z) = z 的圖形。綠色線就是疊代過程:從 z = √2 開始,直走碰到紅線,橫走碰到藍線,再直走碰紅線,再橫走碰藍線,…;綠線每碰到一次紅線,交點的縱座標值就代表做完一層次方的得到的值。可以看出,最後綠線會趨向紅藍線的交點,縱座標值為 2,這也就是說 y = x^(x^(x^(x^(...^x)))) = 2 ,即第三題的情形。
注意:因為綠線一開始是從 z = √2 出發,因此最後會趨近 2 這個解 (左邊的紅藍交點),而不是較大的另一個解 (右邊的紅藍交點,它的值是 4 ,這就是第五題的情況。)。同理,第四題的情形,如果 x = 3√3 ,則 y 應該是較小的 2.478 ,而不是較大的 3;而 y =3 的話 x 就無解。
下圖是放大上圖疊代的部分:
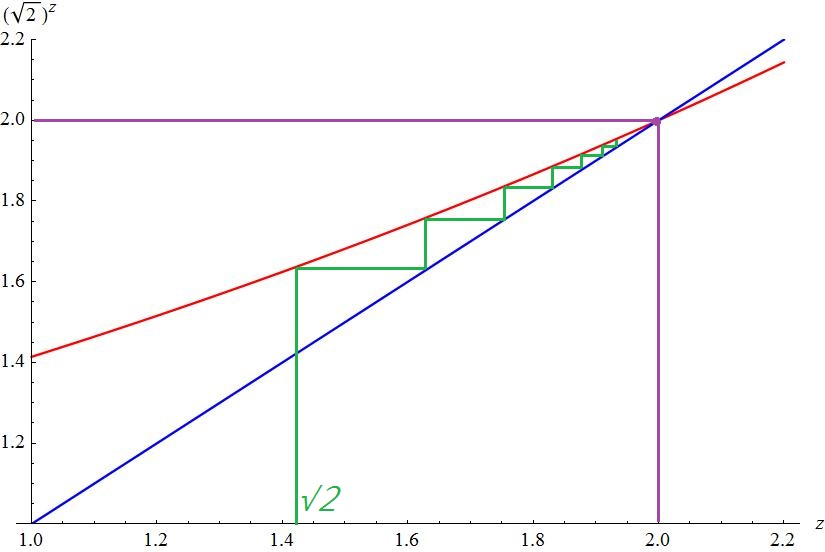
另外,如果 x > e√e ≒ 1.445 ,從最上面的粉紅色線的圖可以看出,不會有 y 的解 (因為超過 y√y 的最大值)。
從疊代法的圖也可以看得出來。注意,當 x > e√e 時,函數 f(z) = xz (紅線) 和 f(z) = z (藍線) 是不會有交點的 (原因要用一點較深的數學,如微積分)。例如,x = 3/2 = 1.5 > 1.445,則疊代圖形如下圖:
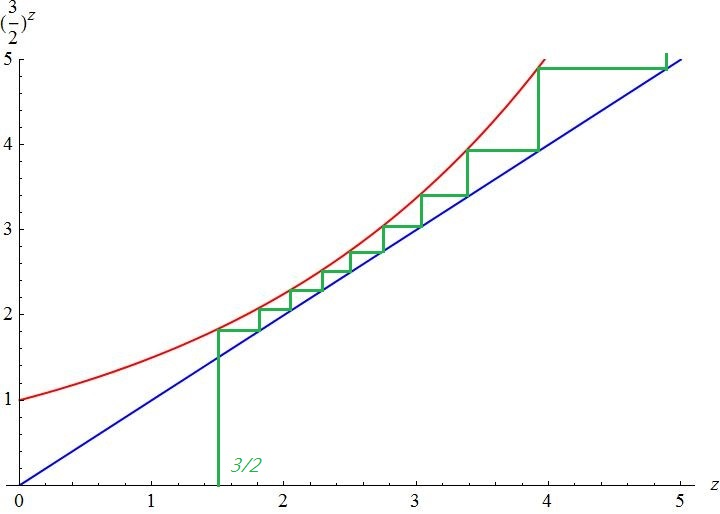
可以看出,因為紅藍線沒有交點,故疊代的綠線就可以一直衝到無限大,不會收斂到有限值。第二題的情形也是如此。
結論:
如果有朋友願意提供完整 (或部分) 的證明,歡迎寫在解析 ~
2) 無限大
3) √2
4) 無解
5) 無解
第一題,不管把 y 算到哪 1 層次方,都是 1 的 1 次方,所以答案還是 1 。
第二題,多算幾層次方就會發現,數字越來越大,而且增大的很快。如:22 = 4 ,24 = 16,216 = 65536,265536 = ……。可以大膽地說是無限大了。
(要證明的話,簡單來說,可以說明每算一層次方,數字至少變成原來的兩倍以上。既然 每次兩倍: 2, 4, 8, 16, ... 最後都會變成無限大,那 y = 2^(2^(2^(...^2))) 當然也是無限大。)
第三題,可用以下方法算出 x:
根據題目, y = x^(x^(x^(x^(...^x)))) ,但是因為有無限個 x 次方,所以:
y = x^(x^(x^(x^(...^x)))) = x^(x^(x^(x^(x^(...^x))))) = x^y = xy
這裡 y = 2 ,故得到 2 = x2 ,所以 x = √2 。 (注意 x 要是正實數)
第四題,如法炮製以上的方法,可得 3 = x3 ,故 x = 3√3 ≒ 1.442 。(3 的立方根)
可惜,這是錯誤的答案。如果真的把 x 代 3√3 去計算 x^(x^(x^(x^(...^x)))) ,多算幾個次方之後,會發現 x^(x^(x^(x^(...^x)))) 的值會趨近 約 2.478 (每多算一層次方,值會越來越大,但是會越來越接近 2.478... 不會再更大。),而不會是 3。
同理,第五題用以上方法得到 x = 4√4 = √2 。但是第三題已經告訴我們, x = √2 時 y 應該要是 2 (而不是 4)。
也可以用另一個看法看出第四、五題算出答案有問題。如果這兩題的解真的就是 3√3 和 4√4 = √2 的話,表示:
3√3^(3√3^…^(3√3)) = 3
√2^(√2^…^(√2)) = 4 ,大於上一行的 3 。
但是,很明顯當 x 越大的時候,y = x^(x^(x^(x^(...^x)))) 也要越大才對,而 3√3 > √2 !表示解一定有哪裡出錯了。
可以見得,看上去類似的問題,貿然用同一招來解的話,常會有誤。
以下說明,給有興趣的朋友參考:
從第三題的做法,可以知道,如果 y 存在 (歷經無限個次方之後仍是有限值,沒有發散),則 y = xy ,也就是 x = y1/y = y√y 。
畫一個 y√y 對 y 的圖:

這個圖形長得很奇怪,主要的特徵如下:
- y = 1 的時候,y√y 也等於 1。
- y = 0 的地方 y√y 無定義,但是 y 趨近於 0 的時候,y√y 也趨近 0。
- y 趨近無限大的時候,y√y 趨近 1 (見上圖)。
- y = e ≒ 2.718 的時候,y√y 會有最大值 e√e ≒ 1.445 。
把圖放大來看:

可以從圖形中看到,當 x = y√y = √2 ≒ 1.414 的時候,y = 2 是一個解 (當然,圖中還看得到右邊有另一個解是 y = 4)。這就符合第三題 (和第五題) 的情形。
第四題的情形,當 x = y√y = 3√3 ≒ 1.442 的時候,y = 3 是一個解 (較大),而 y = 2.478 也是一個解 (較小)。到底哪一個才是對的呢?如上所述實際去計算,得到 y = 2.478 才對,而不是 3 。
如果多試幾種 x, y 值,可以發現,滿足 y = x^(x^(x^(x^(...^x)))) 的 y 值,在圖中總是較小的那個解 (y < e) ,而不會是較大的解 (y > e) 。
如果會疊代法的話,可以看出這一點。例如:x = √2 ,則令函數 f(z) = (√2)z ,一開始 z 代 √2 ,算函數值,然後再代入函數 (其實這就是在一層一層地算次方),重複多次後,就會趨近 y = x^(x^(x^(x^(...^x)))) 。從圖形在看的話,如下圖:

圖中,紅色曲線是 f(z) = (√2)z 的圖形,而藍色直線是 f(z) = z 的圖形。綠色線就是疊代過程:從 z = √2 開始,直走碰到紅線,橫走碰到藍線,再直走碰紅線,再橫走碰藍線,…;綠線每碰到一次紅線,交點的縱座標值就代表做完一層次方的得到的值。可以看出,最後綠線會趨向紅藍線的交點,縱座標值為 2,這也就是說 y = x^(x^(x^(x^(...^x)))) = 2 ,即第三題的情形。
注意:因為綠線一開始是從 z = √2 出發,因此最後會趨近 2 這個解 (左邊的紅藍交點),而不是較大的另一個解 (右邊的紅藍交點,它的值是 4 ,這就是第五題的情況。)。同理,第四題的情形,如果 x = 3√3 ,則 y 應該是較小的 2.478 ,而不是較大的 3;而 y =3 的話 x 就無解。
下圖是放大上圖疊代的部分:

另外,如果 x > e√e ≒ 1.445 ,從最上面的粉紅色線的圖可以看出,不會有 y 的解 (因為超過 y√y 的最大值)。
從疊代法的圖也可以看得出來。注意,當 x > e√e 時,函數 f(z) = xz (紅線) 和 f(z) = z (藍線) 是不會有交點的 (原因要用一點較深的數學,如微積分)。例如,x = 3/2 = 1.5 > 1.445,則疊代圖形如下圖:

可以看出,因為紅藍線沒有交點,故疊代的綠線就可以一直衝到無限大,不會收斂到有限值。第二題的情形也是如此。
結論:
- 當 y > e ≒ 2.718 的時候,y = x^(x^(x^(x^(...^x)))) 無法解出 x 來。
- 當 x > e√e ≒ 1.445 時,y = x^(x^(x^(x^(...^x)))) 不存在 (會趨近無限大而發散)。
如果有朋友願意提供完整 (或部分) 的證明,歡迎寫在解析 ~
12,949
上一道精選數學謎題
下一道精選數學謎題
 A、B 兩人是籃球選手,在同一支球隊。這個賽季中有若干場球賽,每一場 A 與 B 都有上場比求,且每...
A、B 兩人是籃球選手,在同一支球隊。這個賽季中有若干場球賽,每一場 A 與 B 都有上場比求,且每... 跟燒繩子有點類似但後面發展很不同的三部曲,先從簡單的來暖暖身吧~
有五盆一樣多的水,還有五頭喝水速度...
跟燒繩子有點類似但後面發展很不同的三部曲,先從簡單的來暖暖身吧~
有五盆一樣多的水,還有五頭喝水速度... 如果有一個正整數,其組成的位數包含 0~9 所有的十個阿拉伯數字 (例如: 134827653940...
如果有一個正整數,其組成的位數包含 0~9 所有的十個阿拉伯數字 (例如: 134827653940...