5，9，14，21，32，51......(數列一)
如果把(數列一)相鄰兩項的差距寫出來，可得到一數列：
  4，5，7，11，19......(數列二)
其中4=9-5，5=14-9，......以此類推。
看不出(數列二)有甚麼規律嗎？沒關係！
那就把(數列二)相鄰兩項的差距寫出來，可得到一數列：
     1，2，4，8......(數列三)
發現(數列三)是等比數列，其下一項是16！
那就知道(數列二)的下一項是19+16=35
當然也就知道(數列一)的下一項是55+31=86嘍

※：(數列二)為一種差比數列，即：相鄰兩項的差距可形成等比數列的數列。
如果有一種數列，其相鄰兩項的差距可形成一等差數列，則稱其為"二階階差數列"
而等差數列又可說是"一階階差數列"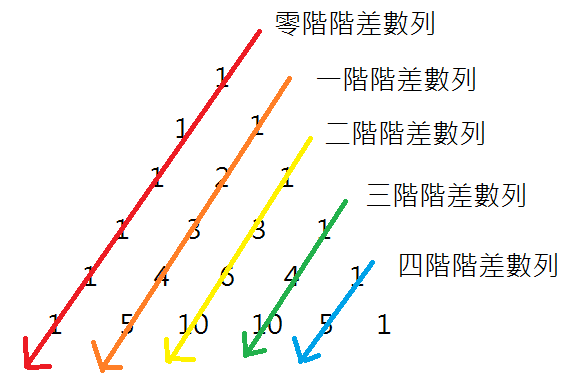感覺有點離題了...