上一道空間概念謎題
下一道空間概念謎題
五連方塊謎題 (Pentomino puzzle)空間概念謎題
答對率:82%
一般人對於俄羅斯方塊(Tetris)應該都不陌生,
俄羅斯方塊其實又稱作「四連方」或者「四格骨牌」(Tetromino),
是由四個全等的正方形所組成,
若考慮鏡像對稱算不同種的話,總共有7種可能的形狀(如圖一),
若考慮鏡像對稱算同一種的話,則只有5種可能的形狀(如圖二)。
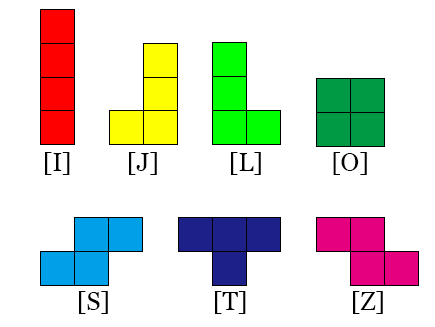
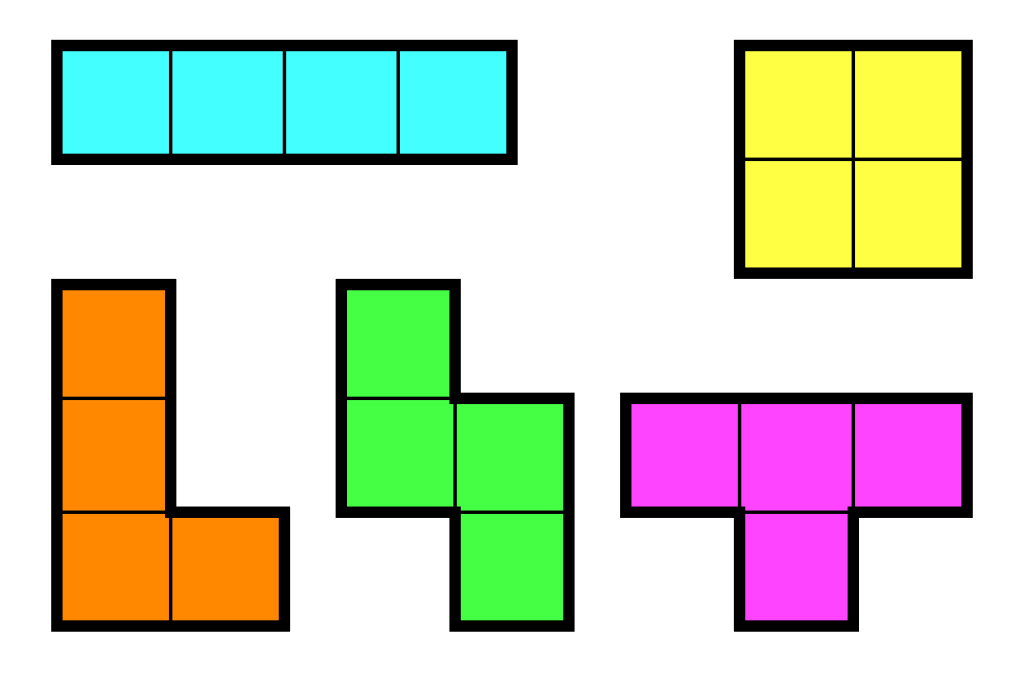
▲圖(一) ▲圖(二)
而今天的謎題用到的則是「五連方」或稱「五格骨牌」(Pentomino),
是由五個全等的正方形所組成,
若考慮鏡像對稱算不同種的話,總共有18種可能的形狀(如圖三),
若考慮鏡像對稱算同一種的話,則只有12種可能的形狀(如圖四)。
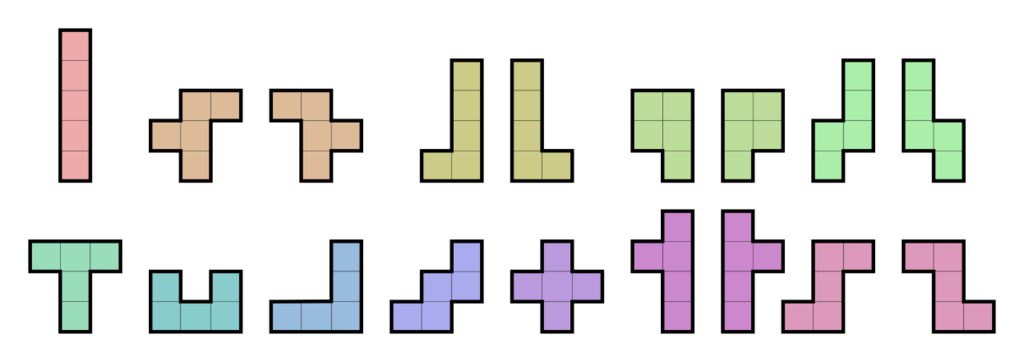
▲圖(三)
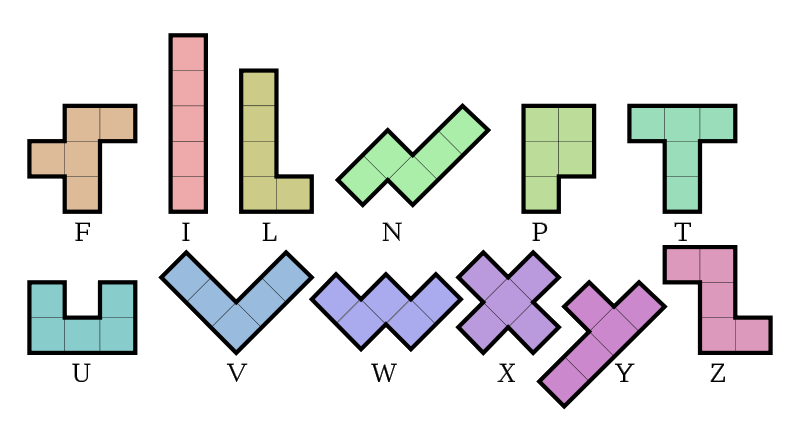
▲圖(四)
圖片來源:維基百科&Google圖片找到的
#謎題:
今天有一個8x8的方格陣如下(別在意線段粗細
 ),
),考慮將前導概念中圖(四)的12種五連方平鋪於其中,
如果規定每個方塊鋪上去時可以翻面也可以旋轉,
但是用過的方塊不能再用,
(換句話說,你手上只有圖(四)的12種五連方各一個,
但鋪上去時可以有如圖(三)的18種形狀)
則請問最少只需要用多少塊五連方,
就能使得其他剩下的五連方都無法平鋪進入8x8的方格陣?
◎請回答最少所需的五連方塊數,並畫出解答圖形作為舉例。
※畫圖方式:你可以下載以下圖片然後利用小畫家的「油漆」填色。
※圖形答案不只一種,如果你有找到跟解析裡不一樣的圖解,
歡迎在留言區附上你的解答圖片網址!

看答案
最少所需的五連方塊數=5 個
解析
我要編輯作者:wangmath99(兆兆) | 歷史版本
※ 溫馨提醒:這次更新版的解析有點長,請有興趣者耐心閱讀

在第一版的解析裡,我給出了「一種組合,八種擺法」,
後來我又在網路上發現國外竟然已經有人提出過這個謎題了!
(我真的是自己想到這題的呀!
 )
)而其中一個相關的PDF檔讓我發現我漏掉了四個擺法,
因此今天(2021/5/2)我在此補上,
同時也補充說明一下第一版解析沒講到的該題的解題邏輯與策略:
本題的基本策略就是要盡可能地「浪費空間」,
而聰明的各位在嘗試舉例一段時間後,應該可以發覺以下三大重點:
1. 由於每個五連方塊各佔5格,所以讓殘留的空間形成四連方塊
(也就是俄羅斯方塊的任一形狀)會是一個還不錯的小策略。
舉例:將「V」字形五連方塊擺放於角落,則可形成一個「O」字形(也就是田字形)
的俄羅斯方塊空間,這樣因為只殘留4格,4<5,所以肯定就放不下了。
(注意:命名代號裡,「L」是指兩臂不等長的直角塊,「V」是指兩臂等長的直角塊)

2. 把12種五連方塊分類為「3x3型」的「正方塊」與「非3x3型」的「瘦長塊」,
(「3x3」是指「會占用到3行3列」,下列圖中「V、W、X」轉45°去看)
則「正方塊」有「F」、「T」、「V」、「W」、「X」、「Z」:
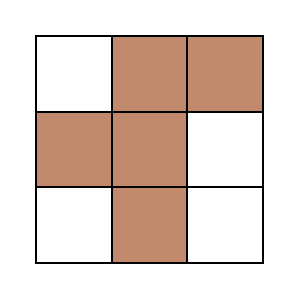
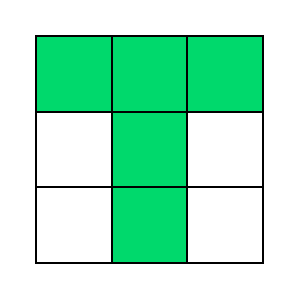
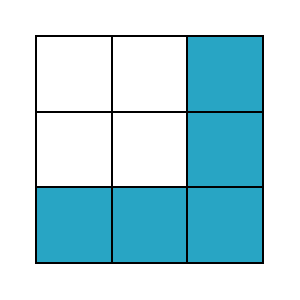
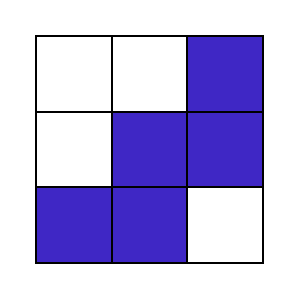
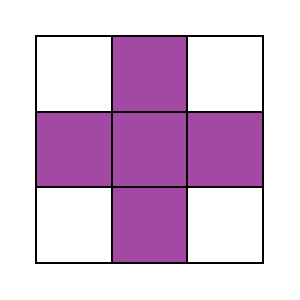
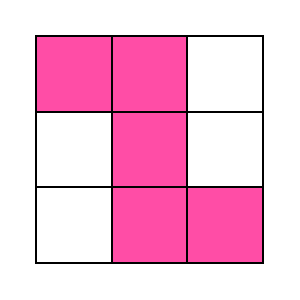
而「瘦長塊」有「I」、「L」、「N」、「P」、「U」、「y」:




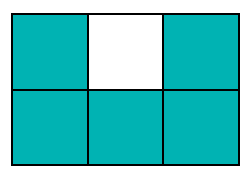

剛好各6塊。我們在多嘗試鋪幾次後可以發現,
在眾多鋪法中,比較難做到讓殘留的空間不出現「細長縫隙」。
因此若都只用3x3型的正方塊,則很容易出現可以讓瘦長塊塞的縫隙。
也就是說,「瘦長塊」大致上比「正方塊」來得容易「鑽縫隙」!
因此,我們可以大概推論,最佳解中「瘦長塊」用上的塊數可能要比較多。
舉例:(失敗案例1)
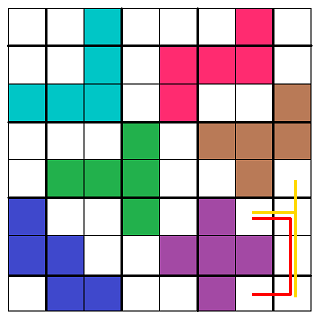
上圖中,我先隨機擺上了所有3x3型的五連方塊,
結果右下角還是出現了「長條空隙」,
可以被「y」字形塊(黃線)或「U」字形塊(紅線)補上。
不過呢,"「瘦長塊」會比較容易「鑽縫隙」"只是「大致上」,
並不是一個精確的說法,因為其實3x3型中的「T」、「V」、「Z」也很能鑽縫隙,
所以真正的關鍵在於殘留空間很容易出現「細長縫隙」!
其中「U」字形塊大概是「最會鑽縫隙」的(P字形塊其次,非嚴謹猜測),
因為它只占用2x3,而且最容易跟任何其他塊緊密嵌合!
所以「U」字形塊最好要用上。
3. 從2.的舉例圖中可以發現中央上方也剛好出現了一個V字形空隙,
但因為V字形塊已經用過了,所以沒有其他塊可以補上去。
因此,盡可能圍出多個自身形狀(也就是用過的五連方形狀)的空隙,也是個好策略。
(重點3.可視為重點1.的推廣版)
綜合以上三大重點,本人想出了以下三大策略:
大策略1:
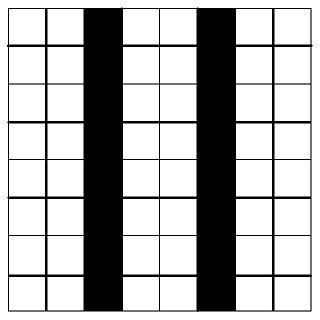
假設我們可以擺出接近上圖的排列,也就是
盡量只佔據第3行和第6行(黑色佔據,白色殘留),
則剩下的「瘦長殘留空間」寬度都只有2且無轉角,
於是3x3型的正方塊就通通都放不下了!
可惜這個大策略1並不能找出最佳解(只用5塊),因為寬度≤2的瘦長塊有6塊!
若少用任何一塊,則那一塊都可以放入寬度為2的那三大行空隙中。
大策略2:
首先先談一談我如何發想出這個策略:
我發現如果把「I」字形塊放在如下圖的靠邊線但不貼邊的位置上,
則其底下會形成只能由「L」或「y」或「N」填補的「極細長空隙」(白線部分)。
(圖中右下角的「y」可換成「S」,也就是翻面後的「N」)

因此,若把近似於「I」字形塊的這些「瘦長塊」
盡量擺在「第二外圈」上(如下圖黑圈部分),
大致「圍出」寬度只有1格的最外邊圈,
則此時由於「瘦長型」塊都已經用掉了,
於是「最外邊圈」這麼多的細長殘留空間就都沒有五連方塊可以填補了!
而中央剩餘的空間則可能拿某一塊一塞就搞定了!
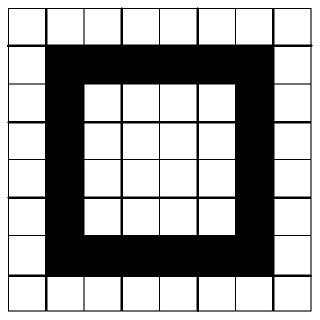
本人嘗試許久後發現很難剛好完美的圍出「第二外圈」,
而且圍完之後還是很容易剛好出現至少一處有得塞的空隙。
以下是其中一個完美圍出「第二外圈」的例子:(失敗案例2)
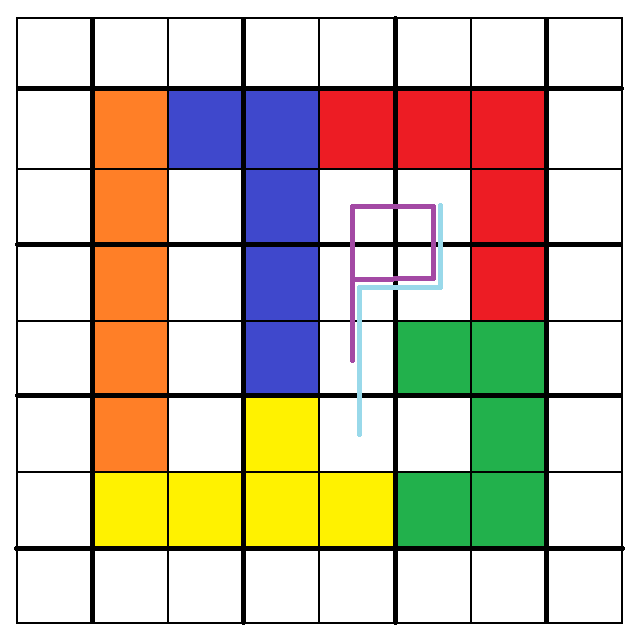
由上圖可看出中央偏右的空隙仍可以塞下「N」或「P」,
然而一旦更換擺法或五連方塊,就會無法圍出完美的第二外圈。
因此我們只好嘗試稍微妥協,允許第二外圈缺一格看看行不行。
此時如果把「U」換成「P」,則剩餘的空間仍可擺下「N」:(失敗案例3)
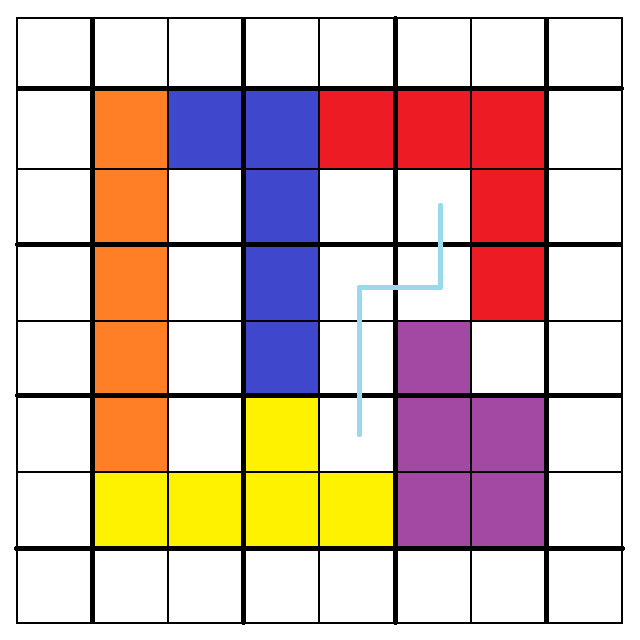
此時如果把「y」換成「N」,則會出現可以擺下「y」的空隙:(失敗案例4)
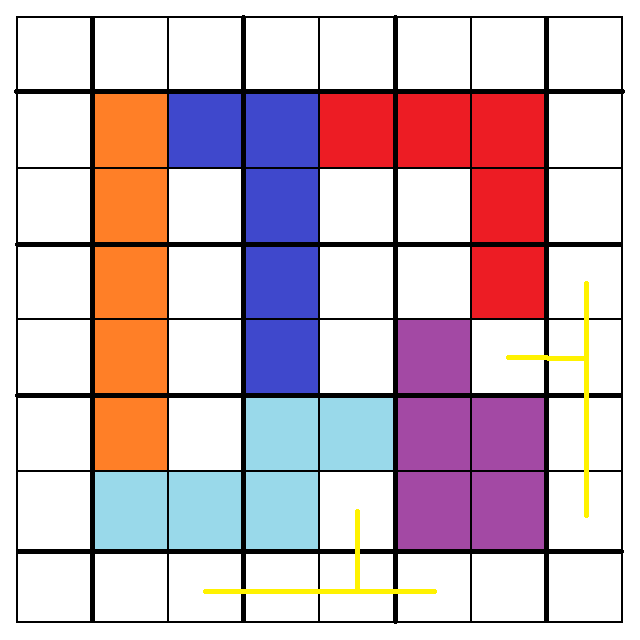
剛剛如果把「U」換成「N」,則又會出現可以擺下「U」的空隙:(失敗案例5)
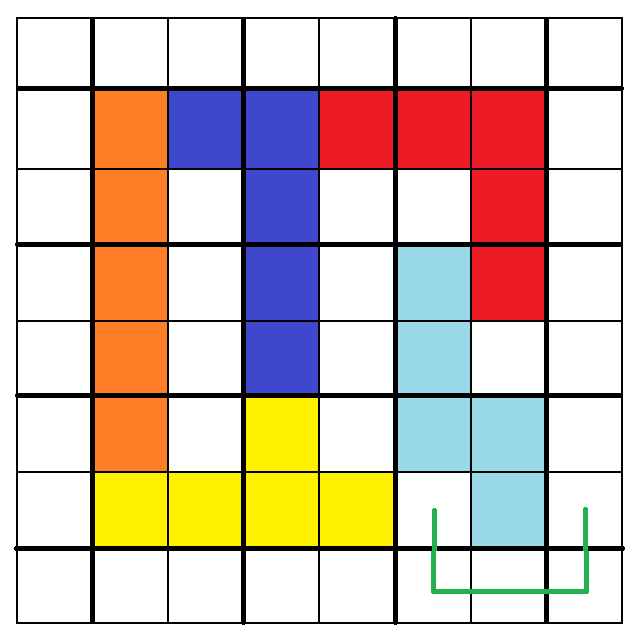
經過多番嘗試都失敗以後,本人終於想到改用以下最終成功的大策略3:

既然第二外圈很容易缺一格,那就乾脆改成
盡量只用瘦長型塊大致圍成如上圖「細長漩渦圈」的形狀!
這麼一來,「由多個『I』、『L』與『V』自身形狀構成的剩餘縫隙」
也形成了細長漩渦狀,可謂把重點3發揮到了極致!
最後只要注意避免中央出現可以讓「P」或「N」塞的空隙即可。
於是,我們終於成功找出了以下「一種組合,十二種擺法」:
1. 2.
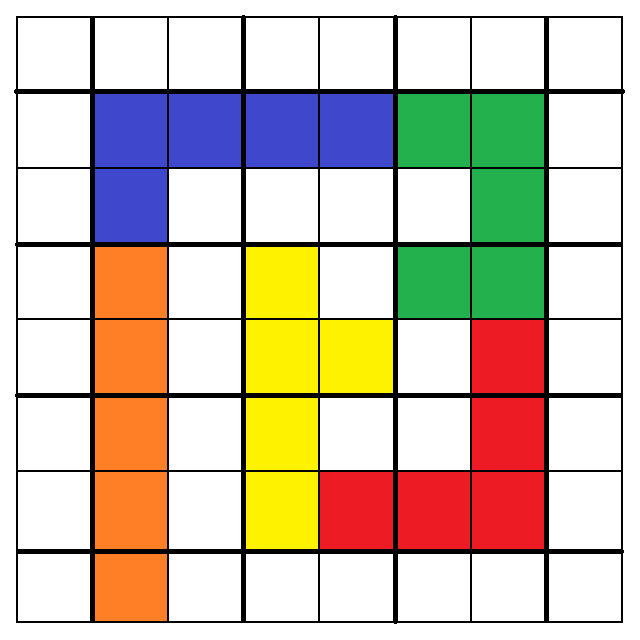
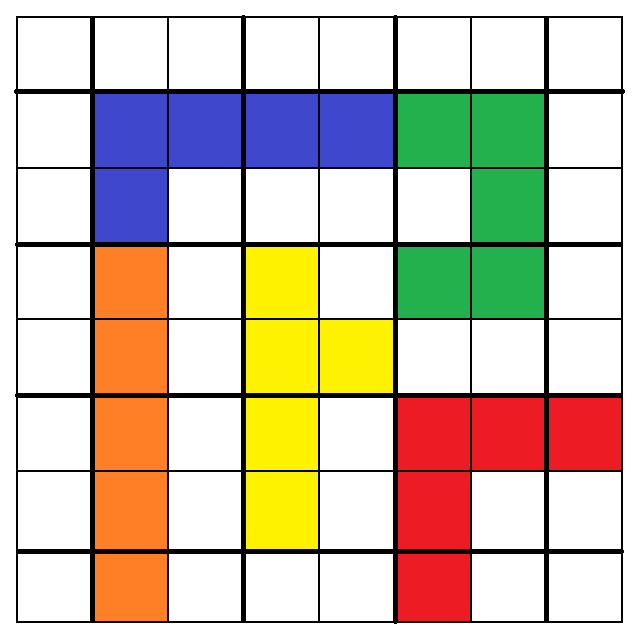
3. 4.
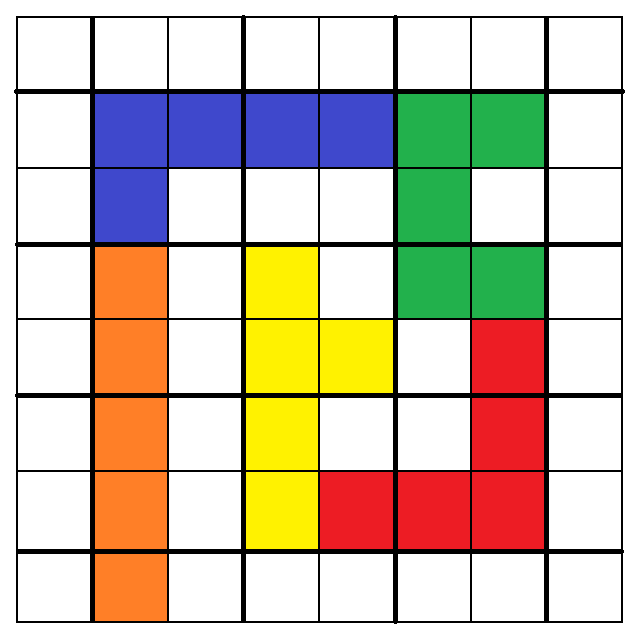
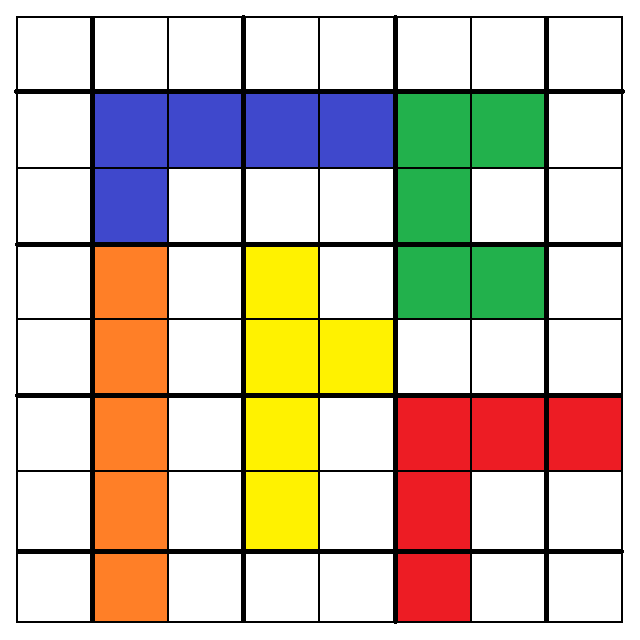
5. 6.
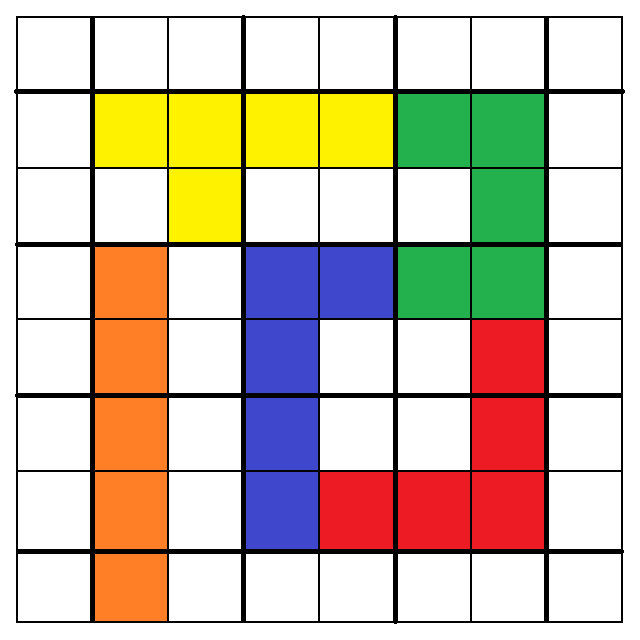
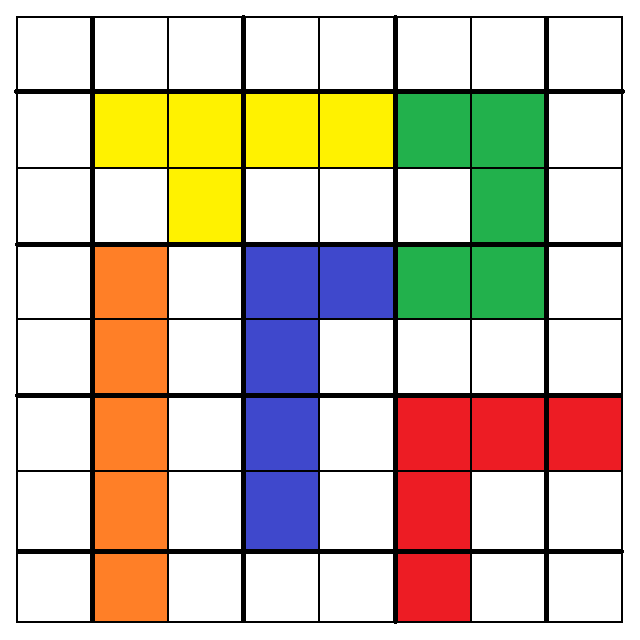
7. 8.
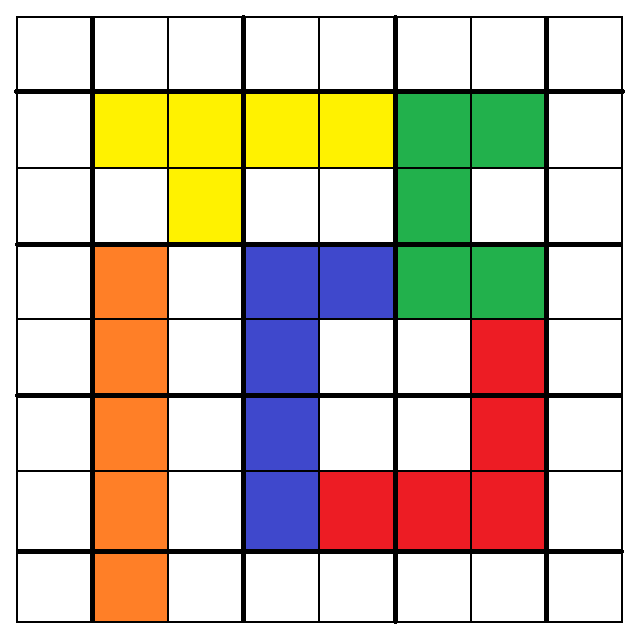
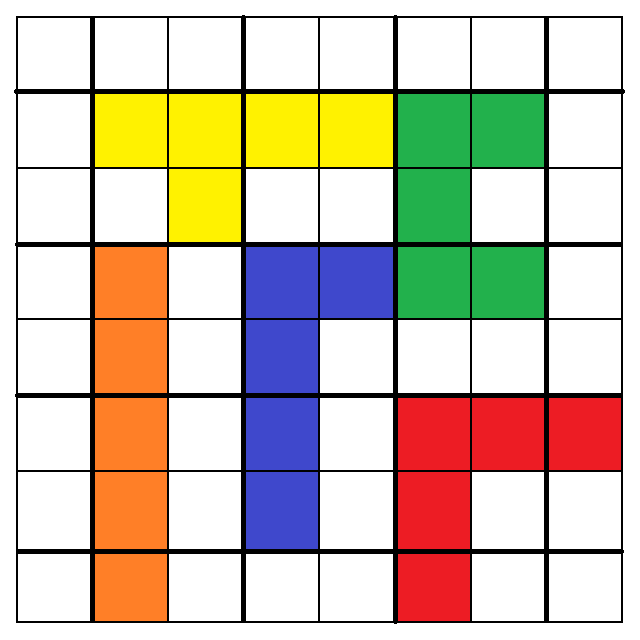
9. 10.
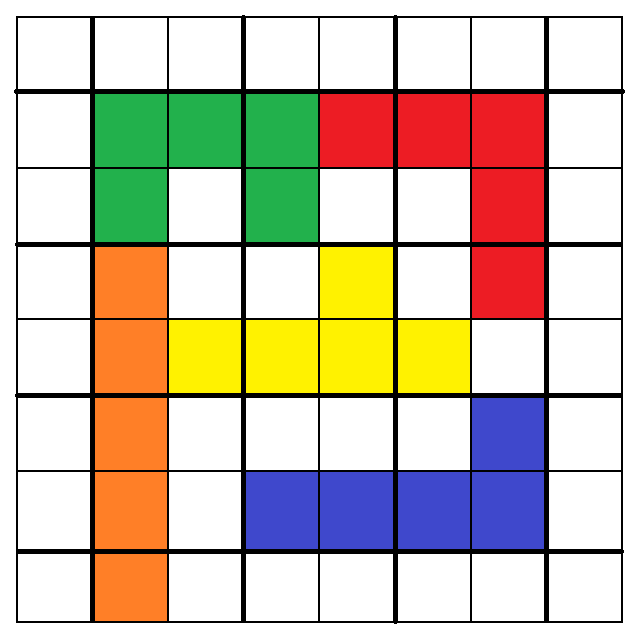
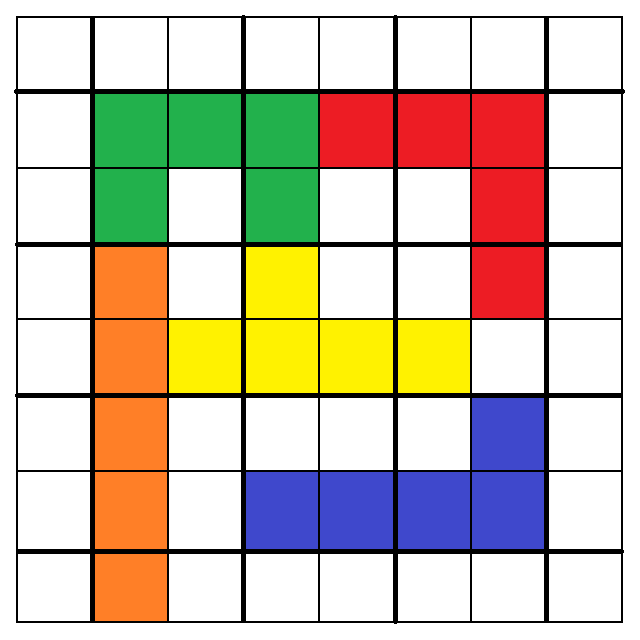
11. 12.
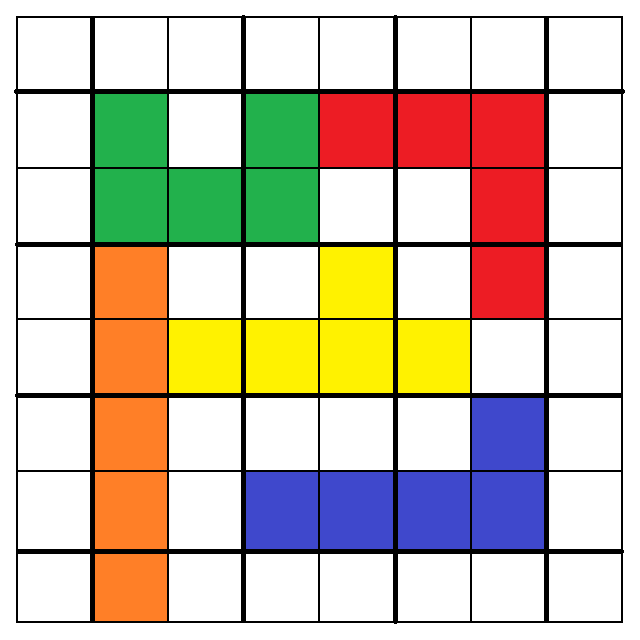
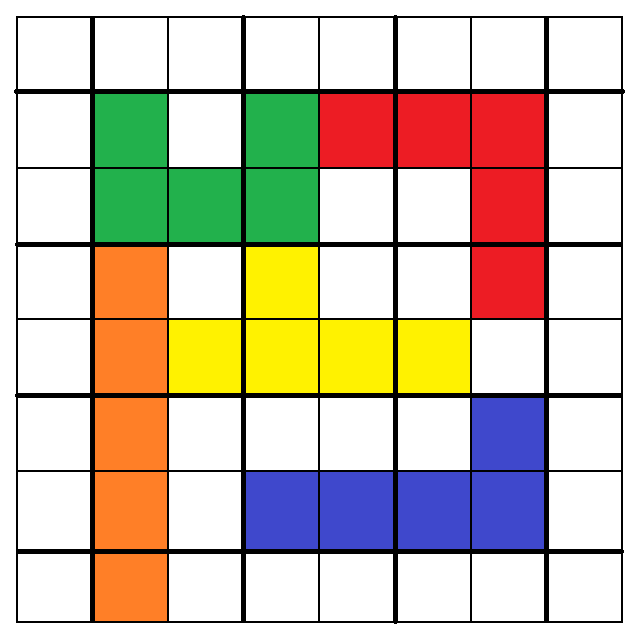
從以上圖中,我們可以看出:
1. 3. 5. 7. 9. 10. 11. 12.大致呈現出最終策略所提及的「細長漩渦圈」形狀,
只有2. 4. 6. 8.例外,也就是我在第一版解析裡漏掉的四種擺法。
其實左右比對一下即可發現,
1.和2.只差在紅色的「V」被改成用重點1.的舉例擺到角落而已,
(同理,3.比對4.也是,5.比對6.也是,7.比對8.也是。)
而左右比對[9.和10.]及[11.和12.]則可發現,換成是黃色的「y」被左右顛倒了而已。
還有上下比對也可以發現,1.和3.只差在綠色的「U」被左右顛倒了而已,
(同理,2.比對4.也是,5.比對7.也是,6.比對8.也是。)
(9.比對11.則是「U」被「上下顛倒」,10.比對12.也是。)
※注意:最後四張的9.~12.都不能變動「V」,否則會出現可以讓「P」或「N」塞的縫隙。
(如下圖,以9.為例)
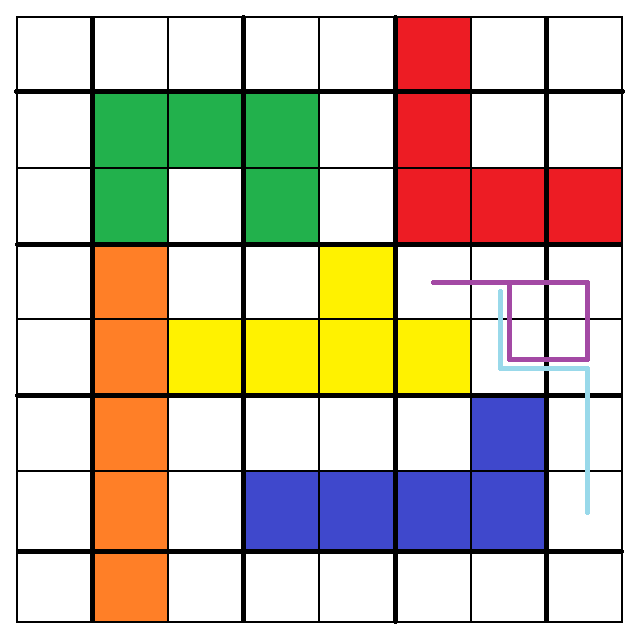
事實上,這12張圖的任何其他變動方式都會產生至少一處的可塞縫隙!
以上就是「I、L、U、V、y」這一組合的十二種擺法,
目前我還未能確定是否就只有這一種組合,
如果有哪位數學或程式設計大神可以幫我驗證的話,我會非常感激~
如果你有找出我沒列出的擺法,也非常歡迎你在留言區貼上圖解的網址!
(可丟到Google雲端硬碟然後用連結分享)
 ~終於寫完惹orz~
~終於寫完惹orz~
6,160
上一道空間概念謎題
下一道空間概念謎題
 承昨天的題目,
有一個人,
他先往南走了1公里,
再往東走了20公里,
再往北走了1公里,
結果居然...
承昨天的題目,
有一個人,
他先往南走了1公里,
再往東走了20公里,
再往北走了1公里,
結果居然...