上一道精選數學謎題
下一道精選數學謎題
托爾斯泰的割草題數學謎題
答對率:85%
《戰爭與和平》的作者托爾斯泰是有名的19世紀末俄國作家,但是很少人知道他還寫過算術課本喔!這題就是他出的有名的計算題~
 一隊割草隊要收割兩塊草地,其中一塊比另一塊大1倍,
一隊割草隊要收割兩塊草地,其中一塊比另一塊大1倍,
割草隊是由訓練有素的割草人組成的,每個人割草的速度都是一樣的;
全隊先用半天時間一起收割大草地,
然後全隊分為人數相同的兩半,一半人繼續留在大草地上割草,另一半人到小草地上割草,
半天又過去了,大草地剛好被割完,小草地還剩下一小部份沒割完,而這一小部份第二天由1個人剛好用一整天割完。
請問這割草隊有幾人?
看答案
8人。
解析
我要編輯大草地=全隊割半天+半隊割半天,也就是等於半隊割1.5天剛好割完;
而小草地面積是大草地的一半,所以小草地需要半隊割0.75天(0.75=1.5/2);
既然小草地在第一天已經被半隊割了半天,所以剩下沒割完的就是半隊割0.25天的量,
半隊割0.25天=一人割1天,所以半隊=4人,
全隊就是8個人啦!
以下畫表再次解釋
| 草地A | 草地B |
如圖,首先,先完成題目的限制
--其中一塊比另一塊大1倍--
假設A比較大
| 草地A(大草地) | 草地B(小草地) |
| X | |
| X | |
| X |
首先抽出草地A(大草地)的收割資料:
--全隊先用半天時間一起收割大草地--(半天)
-- 一半人繼續留在大草地上割草 --(半天)
-- 大草地剛好被割完 --
即草地A(大草地)上午和下午收割的比是2:1
之後抽出草地B(小草地)的收割資料
-- 另一半人到小草地上割草--(半天) --
--小草地還剩下一小部份沒割完,而這一小部份第二天由1個人剛好用一整天割完--
即代入圖表後,由於兩邊各有六格,所以草地A(大草地)的上午收割量和下午收割量是4格和2格
草地B(小草地)的下午收割量=草地A(大草地)下午的收割量,所以草地B也被收割了2格
而且--小草地還剩下一小部份沒割完,而這一小部份第二天由1個人剛好用一整天割完--
因此圖表:
| 草地A(大草地) | 草地B(小草地) |
| 上午 | 下午 |
| 上午 | 下午 |
| 上午 | (一人一天的量) |
| 上午 | X |
| 下午 | X |
| 下午 | X |
由於上述收割量皆是半天,因此把一人一天換成兩人半天,而且因為每格的量皆是相同,所以可以變成:
| 草地A(大草地) | 草地B(小草地) |
| (兩人半天的量)(上午) | (兩人半天的量)(下午) |
| (兩人半天的量)(上午) | (兩人半天的量)(下午) |
| (兩人半天的量)(上午) | (兩人半天的量) |
| (兩人半天的量)(上午) | X |
| (兩人半天的量)(下午) | X |
| (兩人半天的量)(下午) | X |
而上午是出動全隊的,所以只要把上午的人數加起來:
2+2+2+2 =(2×4)=8人
7,920
上一道精選數學謎題
下一道精選數學謎題
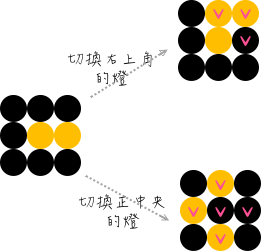 點燈遊戲是一種很常見的益智小品,規則是:
有一些燈並排在一起,每次可切換一個燈的狀態,原本是亮的就會...
點燈遊戲是一種很常見的益智小品,規則是:
有一些燈並排在一起,每次可切換一個燈的狀態,原本是亮的就會... 小傑沒有兄弟姊妹,此刻正孤伶伶的坐在路邊看著一張照片發呆,
路人問他:『你在看誰的照片呀?』小傑回答...
小傑沒有兄弟姊妹,此刻正孤伶伶的坐在路邊看著一張照片發呆,
路人問他:『你在看誰的照片呀?』小傑回答...