上一道精選數學謎題
下一道精選數學謎題
生活數學4-猜拳與機率 (進階題目)數學謎題
答對率:77%
大里高中 林O東 所著
此題你可能會使用(圖片有連結):
說明:
機率是人們在生活中常會碰上的問題,例如:今天的降雨機率、樂透的中獎機率、抽獎的期望值等問題;而猜拳則是人們用來解決分配最好的方法,例如:分配工作時的優先選擇權。當這兩個問題碰在一起,這會產生什麼樣的火花呢?
以下有兩個人猜拳,所有的情況如下:
| 甲 | ||||
| 刀 | 石 | 布 | ||
| 乙 | 刀 | 平手 | 甲勝 | 乙勝 |
| 石 | 乙勝 | 平手 | 甲勝 | |
| 布 | 甲勝 | 乙勝 | 平手 | |
藉由表格我們能看到兩個人出拳時總共有9總可能,而甲乙贏的機率皆為1/3,平手的機率是1/3,也就是兩個人之間能分出勝負的機率是2/3 (66.67%),所以2個人要分出結果非常的容易
提問:
1.請計算3人、4人、5人猜拳時,分出勝負的機率?
2.試以2人猜拳能分出勝負之機率作為a1項,3人猜拳能分出勝負之機率作為a2項,4人猜拳能分出勝負之機率作為a3項,n+1人猜拳能分出勝負之機率作為an項,寫出數列<an>之一般式?
3.當人數超過幾人時,每次猜拳能分出勝負的機率將小於10%?
參考資料:
https://www.youtube.com/watch?v=Kgudt4PXs28&t= (影片資料)
看答案
1.
3人->2/3(67%)
4人->14/27(52%)
5人->10/27(37%)
2.
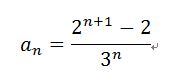
3. 9人以上(含9人)
3人->2/3(67%)
4人->14/27(52%)
5人->10/27(37%)
2.
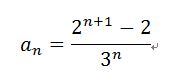
3. 9人以上(含9人)
解析
我要編輯作者:b6d950(東東) | 歷史版本
2人猜拳情形:
分母: 3X3=9
分子:
能分出勝負的有三種情況:剪刀/石頭、石頭/布、布剪/刀
先探討其中一種,剪刀/石頭總共有2種情形,甲-石頭/乙-剪刀 或是 甲-剪刀/乙-石頭
所以兩人猜拳能分出勝負的機率為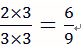
3人猜拳情形:
分母: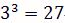
分子:
能分出勝負的有三種情況:剪刀/石頭、石頭/布、布剪/刀
先探討其中一種剪刀/石頭: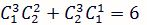
(算式說明: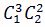 為1刀二石的排列結果,
為1刀二石的排列結果, 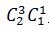 為2刀一石的排列結果)
為2刀一石的排列結果)
再乘上3種情況: 6X3=18
所以三人猜拳能分出勝負的機率為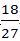
4人猜拳情形:
5人猜拳情形: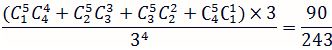
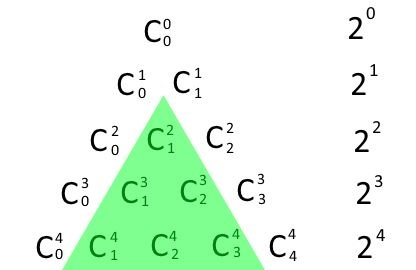
要推出<an>項我們可以借用巴斯卡三角形的性質

他的另一個形式是
我們先討論當a等於2(3人猜拳)時的情況
其中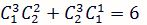 可以發現正好是巴斯卡三角形的第四列減2
可以發現正好是巴斯卡三角形的第四列減2
所以我們可以將式子分子的部分列為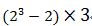
所以整個<a2>項為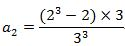
依此類推可以推得他的<a1><a3>及<an>項
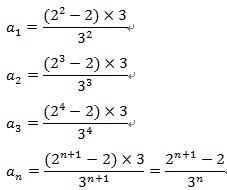
利用上面<an>的公式,我們可以求得當n代入8時(n+1=猜拳的人數),機率會小於10%
解完之後也去看看跟此題一樣探討猜拳的題目吧~猜拳次數的期望值
所以下次有一群人要猜拳時,記得要分開來猜會比較容易得到結果喔^^
分母: 3X3=9
分子:
能分出勝負的有三種情況:剪刀/石頭、石頭/布、布剪/刀
先探討其中一種,剪刀/石頭總共有2種情形,甲-石頭/乙-剪刀 或是 甲-剪刀/乙-石頭
所以兩人猜拳能分出勝負的機率為
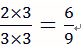
3人猜拳情形:
分母:
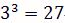
分子:
能分出勝負的有三種情況:剪刀/石頭、石頭/布、布剪/刀
先探討其中一種剪刀/石頭:
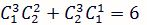
(算式說明:
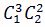 為1刀二石的排列結果,
為1刀二石的排列結果, 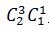 為2刀一石的排列結果)
為2刀一石的排列結果)再乘上3種情況: 6X3=18
所以三人猜拳能分出勝負的機率為
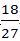
4人猜拳情形:

5人猜拳情形:
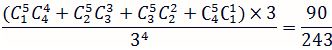
要推出<an>項我們可以借用巴斯卡三角形的性質

他的另一個形式是

我們先討論當a等於2(3人猜拳)時的情況
其中
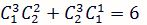 可以發現正好是巴斯卡三角形的第四列減2
可以發現正好是巴斯卡三角形的第四列減2所以我們可以將式子分子的部分列為
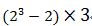
所以整個<a2>項為
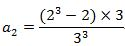
依此類推可以推得他的<a1><a3>及<an>項
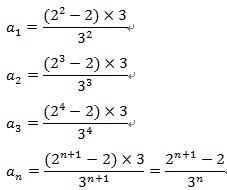
利用上面<an>的公式,我們可以求得當n代入8時(n+1=猜拳的人數),機率會小於10%
解完之後也去看看跟此題一樣探討猜拳的題目吧~猜拳次數的期望值
所以下次有一群人要猜拳時,記得要分開來猜會比較容易得到結果喔^^
11,592
上一道精選數學謎題
下一道精選數學謎題
 有幾名啦啦隊員正在排練隊形,
他們想排出『任兩位隊員之間的距離都是相等的』的隊形,
比如說:三個隊員...
有幾名啦啦隊員正在排練隊形,
他們想排出『任兩位隊員之間的距離都是相等的』的隊形,
比如說:三個隊員... 日期的表示在各個國家有不同的習慣寫法,
比如說1月3日,有些國家習慣寫1.3,有些習慣寫3.1,
常...
日期的表示在各個國家有不同的習慣寫法,
比如說1月3日,有些國家習慣寫1.3,有些習慣寫3.1,
常...