上一道數學謎題
下一道數學謎題
2016數學謎題
答對率:81%
若存在,請找出三組滿足題意的數;若不存在,請解釋您的理由。
看答案
取法很多,以下為其中幾種取法的例子:
(i) 1510個1、504個-1、2、1008
(ii) 1846個1、167個-1、-2、3、336
(iii) 1887個1、125個-1、-2、2、2、252
(iv) 1967個1、44個-1、2、2、2、3、84
(v) 2001個1、9個-1、-2、2、2、3、7、12
(vi) 2001個1、8個-1、2、2、2、3、3、4、7
(i) 1510個1、504個-1、2、1008
(ii) 1846個1、167個-1、-2、3、336
(iii) 1887個1、125個-1、-2、2、2、252
(iv) 1967個1、44個-1、2、2、2、3、84
(v) 2001個1、9個-1、-2、2、2、3、7、12
(vi) 2001個1、8個-1、2、2、2、3、3、4、7
解析
我要編輯作者:Tim930218(凱哥) | 歷史版本
因這2016個數之乘積為2016,故可判斷出這些數中不可能有0;
由2016=2的5次方*3的2次方*7可知它共有6*3*2=36個因數。若這2016個數全部都是正整數,則它們最小的和為2+2+2+2+2+3+7+2008個1=2031,不可能為2016,故這2016個數中必有一些數為負數,且負數的個數必須是偶數個。
若2、2、2、2、2、3、3、7這8個數全為正數,其和為23,其餘2008個數為1或-1,但每多一個數為-1,其和必減少2,故知這八個數的和必為偶數,全部2016個數之和必為奇數,故不合。因此不是1或-1的數之個數為奇數個並且1或-1的數之個數也為奇數個,或不是1或-1的數之個數為偶數個並且1或-1的數之個數也為偶數個。
由2016=2的5次方*3的2次方*7可知它共有6*3*2=36個因數。若這2016個數全部都是正整數,則它們最小的和為2+2+2+2+2+3+7+2008個1=2031,不可能為2016,故這2016個數中必有一些數為負數,且負數的個數必須是偶數個。
若2、2、2、2、2、3、3、7這8個數全為正數,其和為23,其餘2008個數為1或-1,但每多一個數為-1,其和必減少2,故知這八個數的和必為偶數,全部2016個數之和必為奇數,故不合。因此不是1或-1的數之個數為奇數個並且1或-1的數之個數也為奇數個,或不是1或-1的數之個數為偶數個並且1或-1的數之個數也為偶數個。
4,721
上一道數學謎題
下一道數學謎題
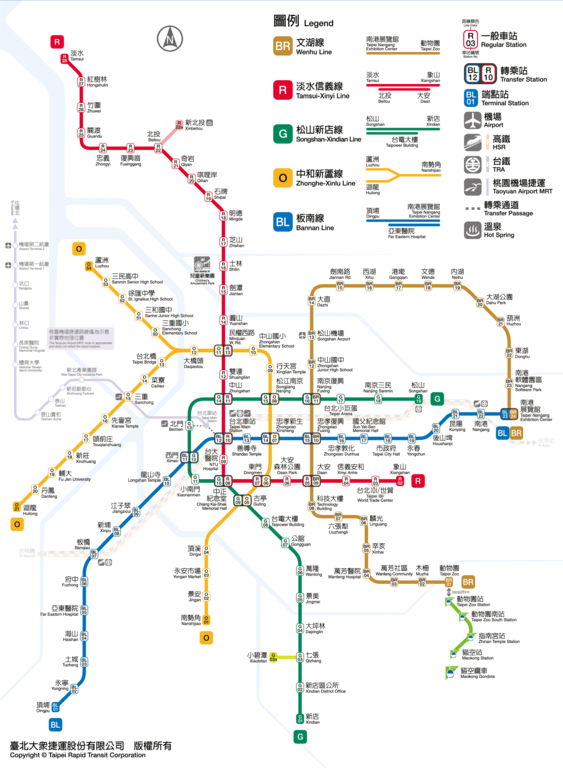 下圖為台北捷運路網圖:圖片來源:http://www.metro.taipei/ct.asp?xIt...
下圖為台北捷運路網圖:圖片來源:http://www.metro.taipei/ct.asp?xIt...