上一道精選邏輯謎題
下一道精選邏輯謎題
愚人節之謎邏輯謎題
答對率:50%
今天正好是愚人節,而你剛好有3個朋友A、B、C在國外
當你和他們傳訊息時,A突然提出了一個難題:
請問:
(一)最少需要問幾次是非題,才能確定我們有幾個人的「今天」是愚人節?
又要問什麼問題呢?
(二)如果把3個朋友改成N個朋友,其他條件相同,那最少要問幾次是非題呢?(以N表示/表示方法可能需用到高中數學)
已知:
1. 這些朋友在愚人節時一定會說謊話,其他日期則一定說實話
2. 每個人互相知道其他人所處的時區,但你並不知道,而且你也不知道他們所處的時區是否相同
3. 問兩個人相同的問題視為問兩次;問三個人相同的問題視為問三次;以此類推
4. 只要確定幾個人就好,不用確定是誰
5. 請不要問一些可能沒辦法回答的問題(例:請問這題的答案是否定的嗎?)

5. 請不要問一些可能沒辦法回答的問題(例:請問這題的答案是否定的嗎?)

看答案
(一)2個 詳細問題見解析
(二) 其中[x]為高斯函數,代表小於等於x的最大整數
其中[x]為高斯函數,代表小於等於x的最大整數
(二)
解析
我要編輯作者:jerry1021dd(章魚~) | 歷史版本
(一)
要問3個朋友中有幾個人今天是愚人節,則有4種可能的答案:0,1,2,3個
既然有4種答案 則表示最少要問2個是非題 (第一題有兩種回答*第二題有兩種回答=4種結果)
也就是說,每一種問題的回答都要刪掉兩種可能
於是可以問A以下這兩個問題
「如果我問你『三人中今天是愚人節的人數至少兩人嗎?』你會回答 是 嗎?」
「如果我問你『三人中今天是愚人節的人數是奇數個嗎?』你會回答 是 嗎?」
不論A說真話或假話,他回答出來的一定是雙引號內正確的答案。
於是可以做出回答和人數的對照
(是,是) --> 3人
(是,否) --> 2人
(否,是) --> 1人
(否,否) --> 0人
(二)
其實如果秉持著第一題的原則
不難發現每次問題都可以刪掉一半的可能 於是知道等一下可能會需要用到log(以2為底)
回到第二題,如果有N個人,那麼答案就會有N+1種可能(0,1,2,...,N)
但是要注意 如果令N+1=2k (k是正整數)
那麼2k-1和2k問的次數會一樣(都是k);2k+1則需要多問一次(k+1)
所以,待會在用高斯符號前需要讓(N+1)先-1
才能2k-1和2k取log和高斯後所得到的值一樣
最後再把當初扣掉的1加回來即可
於是變成-1)%5D+1)
化簡得
要問3個朋友中有幾個人今天是愚人節,則有4種可能的答案:0,1,2,3個
既然有4種答案 則表示最少要問2個是非題 (第一題有兩種回答*第二題有兩種回答=4種結果)
也就是說,每一種問題的回答都要刪掉兩種可能
於是可以問A以下這兩個問題
「如果我問你『三人中今天是愚人節的人數至少兩人嗎?』你會回答 是 嗎?」
「如果我問你『三人中今天是愚人節的人數是奇數個嗎?』你會回答 是 嗎?」
不論A說真話或假話,他回答出來的一定是雙引號內正確的答案。
於是可以做出回答和人數的對照
(是,是) --> 3人
(是,否) --> 2人
(否,是) --> 1人
(否,否) --> 0人
(二)
其實如果秉持著第一題的原則
不難發現每次問題都可以刪掉一半的可能 於是知道等一下可能會需要用到log(以2為底)
回到第二題,如果有N個人,那麼答案就會有N+1種可能(0,1,2,...,N)
但是要注意 如果令N+1=2k (k是正整數)
那麼2k-1和2k問的次數會一樣(都是k);2k+1則需要多問一次(k+1)
所以,待會在用高斯符號前需要讓(N+1)先-1
才能2k-1和2k取log和高斯後所得到的值一樣
最後再把當初扣掉的1加回來即可
於是變成
化簡得
27,762
上一道精選邏輯謎題
下一道精選邏輯謎題
 右邊是城堡平面圖,原題目是將所有的小路都填滿雪水,而以下改變一點規則:
假設這些古堡中的道路上每個住...
右邊是城堡平面圖,原題目是將所有的小路都填滿雪水,而以下改變一點規則:
假設這些古堡中的道路上每個住...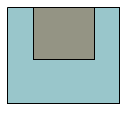 有一個立體物品,從頂面看和從正面看到的都是如下的樣子:
你能畫出這個立體物品實際長什麼樣子嗎?
有一個立體物品,從頂面看和從正面看到的都是如下的樣子:
你能畫出這個立體物品實際長什麼樣子嗎?