上一道精選數學謎題
下一道精選數學謎題
twelve, thirty, ninety (12, 30, 90)數學謎題
答對率:62%
這類型的題目大家可能常看到,但這題可不簡單喔,有五顆星呢!
12+12+12+12+12+30=90,這是個簡單的算式,
翻成英文寫成直式就是:
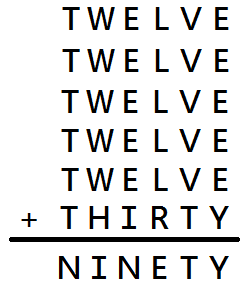
其中每個英文字母代表0~9的數字且不重複,
請解出每個英文字母代表的數字,讓等式依然成立。
看答案
TWELVE=130760
THIRTY=194215
NINETY=848015
解析
我要編輯首先先觀察最左邊那排T。六個T相加(並考慮可能的進位)等於N,表示六個T相加並不會進位。因此T只可能是0、1。但T又是數字最左邊的位數,而數字不能以0開頭,所以T只可能是1。
然後觀察個位數的那排E。5個E相加,再加上Y,但個位數卻還是Y。這表示5E的尾數為0,因此E只可能是偶數的0、2、4、6、8。然後從上面得知T=1。5個V加上1再加上個位數的進位,但剩下的十位數卻還是1,表示從個位數過來的進位,不是0就是5(因為不論V為何,5V的尾數不是0就是5;而這個尾數與個位數的進位相加,新的位數必須等於0)。唯一滿足此條件的偶數只有0,故解出E=0。另外,Y以任何數字帶入,算式都會成立。
解出E=0後,觀察千位數那排數字。因為E=0,所以I加上百位數的進位等於N。因為T=1,且W≧2,N至少等於7。如果千位數有進位,那I+百位數的進位至少要等於17。但百位數最多也只能進位6,而I不可能大於10,所以可以得知千位數並沒有發生進位。
所以現在算式,帶入已解出的字母,可以拆成兩部分:
1W 0LV0
+1W +0LV0
+1W +0LV0
+1W +0LV0
+1W +0LV0
+1H +IR1Y
----------
NI N01Y
接下來,分別測試可能性來篩選出正確的答案。
觀察W。因為千位數沒有進位,所以I一定是5W+H的尾數。因為H≠I,所以W只可能是奇數的3、5、7、9。但因為十萬位數沒有發生進位,所以W不可能是9。剩下的可能性有3、5、7。
假設W=7,N則為9,且H+5=I(不可進位)。因此H只可能是2、3。此假設下I≧7,又I+百位數進位=9。這代表百位數進位不能超過2。此時觀察十位數:5V+1的尾數還是1(因為個位數沒有進位),表示V只能是偶數,因此進位的可能有1、2、3、4(V分別為2、4、6、8)。觀察百位數:5L+R+十位數進位的尾數是0。因為百位數的進位不能大於2,因此L剩下可能只有2、3(如果L=4,因為R+十位數的進位尾數必須也是0,百位數的進位就會變成3)。另外,因為0與1已知,所以百位數的進位至少有2(5L本身至少會進位1;然後5L的尾數+十位數的進位+R,尾數必須是0,所以一定會再發生一次進位)。
和先前一樣,因為百位數的進位至少有2,所以I至少要比N小2。W=3的情況下,如果5+H沒有進位,那N一定是7;沒有進位的情況下H、I的可能有H=3,I=8、H=4,I=9兩種,但沒有一種的I至少比N小2,所以接下來只需要考慮進位的情況,且在進位的情況下,N只可能是8,因此N=8。
考慮到近位的情況下,H與I只有以下兩種可能:H=7,I=2、H=9,I=4。
此時帶入已知的數字,算式看起來如下:
13 0LV0
+13 +0LV0
+13 +0LV0
+13 +0LV0
+13 +0LV0
+19 +4R1Y
----------
84 801Y
觀察百位數與千位數,得知百位數的進位必須是4。又5L+十位數的進位+R,尾數必須是0,因此得知5L必須進位三次。此條件下,L只可能是6、7。
L=7,這表示R+十位數進位=5。現在未使用的數字只有2、5、6三個。R必須小於5,因此得知R=2。又因為R=2,十位數進位必需是3,而滿足此條件的只有V=6,故得知。
現在唯一沒使用過的數字就是5,因此得知Y=5。
然後觀察個位數的那排E。5個E相加,再加上Y,但個位數卻還是Y。這表示5E的尾數為0,因此E只可能是偶數的0、2、4、6、8。然後從上面得知T=1。5個V加上1再加上個位數的進位,但剩下的十位數卻還是1,表示從個位數過來的進位,不是0就是5(因為不論V為何,5V的尾數不是0就是5;而這個尾數與個位數的進位相加,新的位數必須等於0)。唯一滿足此條件的偶數只有0,故解出E=0。另外,Y以任何數字帶入,算式都會成立。
解出E=0後,觀察千位數那排數字。因為E=0,所以I加上百位數的進位等於N。因為T=1,且W≧2,N至少等於7。如果千位數有進位,那I+百位數的進位至少要等於17。但百位數最多也只能進位6,而I不可能大於10,所以可以得知千位數並沒有發生進位。
所以現在算式,帶入已解出的字母,可以拆成兩部分:
1W 0LV0
+1W +0LV0
+1W +0LV0
+1W +0LV0
+1W +0LV0
+1H +IR1Y
----------
NI N01Y
接下來,分別測試可能性來篩選出正確的答案。
觀察W。因為千位數沒有進位,所以I一定是5W+H的尾數。因為H≠I,所以W只可能是奇數的3、5、7、9。但因為十萬位數沒有發生進位,所以W不可能是9。剩下的可能性有3、5、7。
假設W=7,N則為9,且H+5=I(不可進位)。因此H只可能是2、3。此假設下I≧7,又I+百位數進位=9。這代表百位數進位不能超過2。此時觀察十位數:5V+1的尾數還是1(因為個位數沒有進位),表示V只能是偶數,因此進位的可能有1、2、3、4(V分別為2、4、6、8)。觀察百位數:5L+R+十位數進位的尾數是0。因為百位數的進位不能大於2,因此L剩下可能只有2、3(如果L=4,因為R+十位數的進位尾數必須也是0,百位數的進位就會變成3)。另外,因為0與1已知,所以百位數的進位至少有2(5L本身至少會進位1;然後5L的尾數+十位數的進位+R,尾數必須是0,所以一定會再發生一次進位)。
接下來檢視W=7的假設下,僅有的兩種可能:
- H=2,I=7: W已經是7了,故I不可為7。
- H=3,I=8:因為百位數的進位至少有2,8+2>9,所以假設無法成立。
因此W不可能是7。此時W只剩下兩種可能:3、5。
現在假設W=5。由先前的經驗得知,因為百位數的進位至少有2,所以I至少要比N小2。5+H如果沒有進位,那麼N一定等於8。但H與I的所有可能:H=2,I=7;H=3,I=8;H=4,I=9都無法滿足I至少比N小2的條件。所以如果W=5成立,那5+H一定有發生進位,且N=9。只考慮進位的情況,H與I有以下兩種可能:H=7,I=2、H=8,I=3。
現在假設W=5。由先前的經驗得知,因為百位數的進位至少有2,所以I至少要比N小2。5+H如果沒有進位,那麼N一定等於8。但H與I的所有可能:H=2,I=7;H=3,I=8;H=4,I=9都無法滿足I至少比N小2的條件。所以如果W=5成立,那5+H一定有發生進位,且N=9。只考慮進位的情況,H與I有以下兩種可能:H=7,I=2、H=8,I=3。
- H=7,I=2:I+百位數進位等於N。現在考慮百位數最大進位可能:L最大可為8,因此5L=40→4次進位;又R+十位數進位只能再多一次進位,所以最大進位可能是5。在I=2、N=9的情況下,假設無法成立。
- H=8,I=3:跟上面相似,在I=3、N=9的情況下,百位數的最大進位可能是4,因此假設無法成立。
和先前一樣,因為百位數的進位至少有2,所以I至少要比N小2。W=3的情況下,如果5+H沒有進位,那N一定是7;沒有進位的情況下H、I的可能有H=3,I=8、H=4,I=9兩種,但沒有一種的I至少比N小2,所以接下來只需要考慮進位的情況,且在進位的情況下,N只可能是8,因此N=8。
考慮到近位的情況下,H與I只有以下兩種可能:H=7,I=2、H=9,I=4。
- H=7,I=2:I+百位數的進位=N,又I=2、N=8,這表示百位數至要進位6。但與先前的方法類似:L最高可能是9,5L=45→進位四次,再加上尾數的5+十位數進位+R可以再進位一次,百位數最高的進位也只有5,無法達到6。因此假設無法成立。
- H=9,I=4:因為上面的可能無法成立,因此H=9,I=4是剩下的唯一可能。
此時帶入已知的數字,算式看起來如下:
13 0LV0
+13 +0LV0
+13 +0LV0
+13 +0LV0
+13 +0LV0
+19 +4R1Y
----------
84 801Y
觀察百位數與千位數,得知百位數的進位必須是4。又5L+十位數的進位+R,尾數必須是0,因此得知5L必須進位三次。此條件下,L只可能是6、7。
- L=6:如果L=6,那R+十位數進位就必須等於10。剩下的數字有2、5、7。又因為V必須是偶數,所以十位數的進位只可能是1。9已經被佔走,所以R無解。因此假設無法成立。
- L=7:因為L=6無法成立,所以L只能是7。
L=7,這表示R+十位數進位=5。現在未使用的數字只有2、5、6三個。R必須小於5,因此得知R=2。又因為R=2,十位數進位必需是3,而滿足此條件的只有V=6,故得知。
現在唯一沒使用過的數字就是5,因此得知Y=5。
8,924
上一道精選數學謎題
下一道精選數學謎題
 據報,一名走私販帶著大量現金搭上了特快車,
這班車中途都沒有停靠站,一路直達目的地,
警方隨即派人埋...
據報,一名走私販帶著大量現金搭上了特快車,
這班車中途都沒有停靠站,一路直達目的地,
警方隨即派人埋... 兩人同行,前不著村,後不著店。
(射一字)
兩人同行,前不著村,後不著店。
(射一字)
 這題字謎有兩個答案,但解法都是五星級的喔!
子丑寅卯辰巳午未申酉亥
(射一字;但有兩個答案都通)
...
這題字謎有兩個答案,但解法都是五星級的喔!
子丑寅卯辰巳午未申酉亥
(射一字;但有兩個答案都通)
... 這題是在測驗智力,還是在測驗個性呢?也許沒有標準解答,快來說說你的答案吧!
一個暴風雨的夜晚,你獨自...
這題是在測驗智力,還是在測驗個性呢?也許沒有標準解答,快來說說你的答案吧!
一個暴風雨的夜晚,你獨自...