上一道數學謎題
下一道數學謎題
被11111整除的10位數數學謎題
答對率:74%
且可以被11111整除,則此10位數為?
看答案
答案很多,僅舉出一組例子。
1056789432
1056789432
解析
我要編輯把這 10 位數的每一位加起來,1+2+3+4+5+6+7+8+9+0=45,根據 9 的倍數判定法,45 能被 9 整除,所以這個數字一定是 9 的倍數,再加上題目說這是 11111 的倍數,那這個數就是 99999 的倍數。
接下來可以注意到 99999 的 1~100000 倍是:
0000099999、0000199998、0000299997、...、0000999990、
0001099989、0001199988、...、0009999900、0010099899、...、9999900000,
也就是 99999 的 x 倍(限1~100000)的前 5 位數是 x-1,並且前 5 位和後 5 位加起來是 99999,以式子來表達就是 99999x=100000(x-1)+(99999-(x-1))。
湊一個滿足條件的 10 位數的方法應該就很清楚了,1 位對 6 位、2 位對 7 位、3 位對 8 位、4 位對 9 位、5 位對 10 位(右到左 1~10位),0 對 9、1 對 8、2 對 7、3 對 6、4 對 5,例如:5678943210。
接下來可以注意到 99999 的 1~100000 倍是:
0000099999、0000199998、0000299997、...、0000999990、
0001099989、0001199988、...、0009999900、0010099899、...、9999900000,
也就是 99999 的 x 倍(限1~100000)的前 5 位數是 x-1,並且前 5 位和後 5 位加起來是 99999,以式子來表達就是 99999x=100000(x-1)+(99999-(x-1))。
湊一個滿足條件的 10 位數的方法應該就很清楚了,1 位對 6 位、2 位對 7 位、3 位對 8 位、4 位對 9 位、5 位對 10 位(右到左 1~10位),0 對 9、1 對 8、2 對 7、3 對 6、4 對 5,例如:5678943210。
6,041
上一道數學謎題
下一道數學謎題
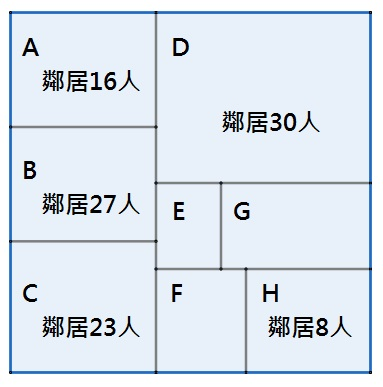 在一正方形土地上住著8戶人家,請依照以下條件找出每戶家裡人數?
(1)A~H分別住了3~10人,每戶...
在一正方形土地上住著8戶人家,請依照以下條件找出每戶家裡人數?
(1)A~H分別住了3~10人,每戶... 三胞胎正在罰站被問話,因為媽媽心愛的花瓶被打破了,
爸爸說他吃午飯前看到花瓶還好好的,吃完午飯後就看...
三胞胎正在罰站被問話,因為媽媽心愛的花瓶被打破了,
爸爸說他吃午飯前看到花瓶還好好的,吃完午飯後就看... 這題你能多快算出答案呢?
小楷、小治去逛玩具店,都想買同一個玩具,
可惜,小楷不夠1元,小治不夠10...
這題你能多快算出答案呢?
小楷、小治去逛玩具店,都想買同一個玩具,
可惜,小楷不夠1元,小治不夠10... 這題列在快問快答,請大家試著用盡量簡便的方式把答案算出來喔!
小楷、小治兩人在泳池游泳,
兩人同時同...
這題列在快問快答,請大家試著用盡量簡便的方式把答案算出來喔!
小楷、小治兩人在泳池游泳,
兩人同時同...