上一道精選數學謎題
下一道精選數學謎題
數字magic數學謎題
答對率:95%
在下列6個○中,填入1~6,6個數字,數字不重複,使每條線總和相等。
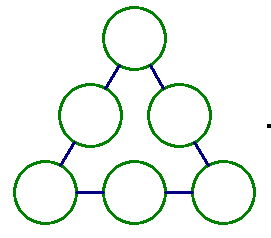
挑戰2 正方
在下列8個○中,填入1~8,8個數字,數字不重複,使每條線總和相等。
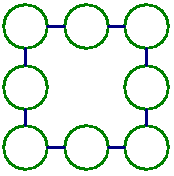
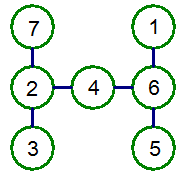
挑戰3 H
在下列7個○中,填入1~7,7個數字,數字不重複,使每條線總和相等。
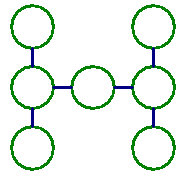
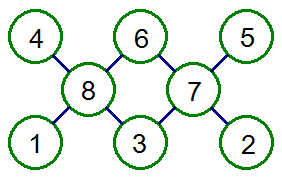
挑戰4 double X
在下列8個○中,填入1~8,8個數字,數字不重複,使每條線總和相等。
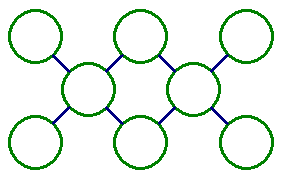
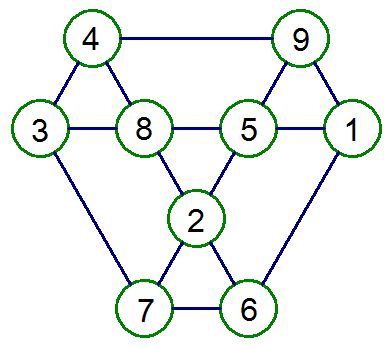
挑戰5 diamond
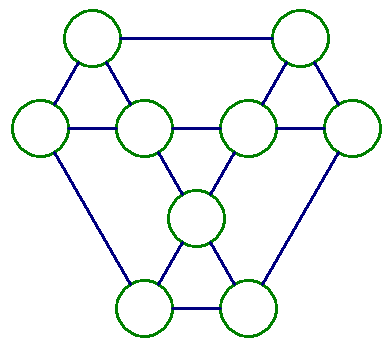
在下列9個O中,填入1~9,9個數字,數字不重複,使每個正三角形三頂點和相等。(共七個正三角形)
挑戰六 奧運五圓
由五個圓構成a、b、c、d、e、f、g、h、i九個區域,在九個區域填入1~9,9個數字,數字不重複,使每一個圓環內的和都相等。
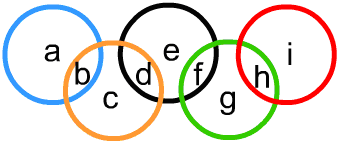
看答案
我會再po
解析
我要編輯參考答案
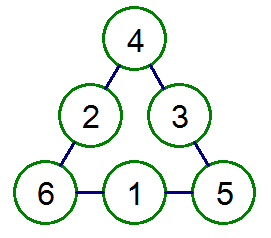
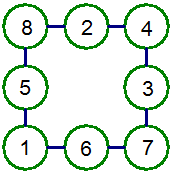
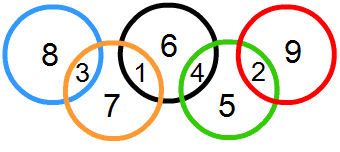
分析
因此我會先假設關鍵位置的數字並確認總和,再安排剩餘數字,失敗了就換下一組。
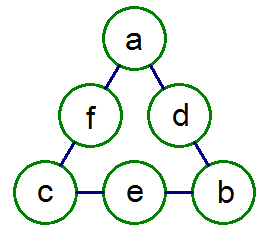 挑戰1: 正三角
挑戰1: 正三角假設每條線的和都是X,可列出
a+b+d=X, a+c+f=X, b+c+e=X
並且我們知道a~f介在1~7而且不重複,
三式相加2a+2b+2c+d+e+f
=a+b+c+(a+b+c+d+e+f)=a+b+c+21=3X
得到X=(a+b+c+21)/3,
因此a+b+c必須是3的倍數。
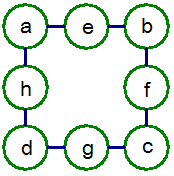
挑戰2: 正方
同挑戰1的解法,
可得出X=(a+b+c+d+36)/4,
因此a+b+c+d必須是4的倍數。
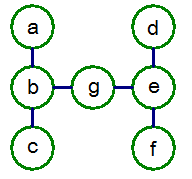
挑戰3: H
同挑戰1的解法,
可得出X=(b+e+28)/3,
因此b+e必須是3的倍數+2。
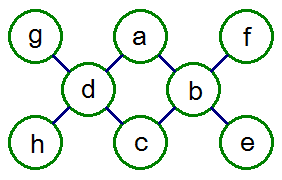
挑戰4: double X
事實上這題和挑戰2是一樣的題目,
注意到四條線都是a+b+e, a+d+h, b+c+f, c+d+g。
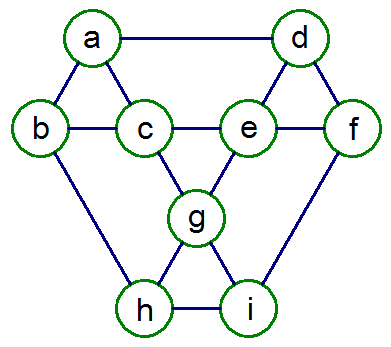
挑戰5: diamond
三角形abc,def,ghi恰好涵蓋a~i,
可知三角形的和都是45/3=15。
接著注意到c,e,g,
它們都被三個三角形涵蓋到,
那麼c,e,g不會是1,3,7,9中的任一個,
因為包含它們又要湊到15只有兩種方式
(像包含3就只有3+4+8=3+5+7=15)。
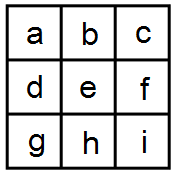 儘管規則有一些變化,
儘管規則有一些變化,但這題的結構和九宮格幾乎一樣,
差別只在於少了對角線aei的和要15。
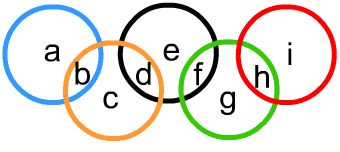
挑戰6:奧運五圓
同挑戰1的解法,
可得出X=(b+d+f+h+45)/5,
因此b+d+f+h必須是5的倍數。
28,721
上一道精選數學謎題
下一道精選數學謎題
 老師出了五題題目給全班50個人回答,
第一題有40個人答對,
第二題有30個人答對,
第三題有31個...
老師出了五題題目給全班50個人回答,
第一題有40個人答對,
第二題有30個人答對,
第三題有31個...