上一道精選數學謎題
下一道精選數學謎題
好槍?爛槍?數學謎題
答對率:72%
不過,這個走私集團走私來的槍枝品質向來堪虞 (有礙於你們幫的經濟買不起太高級的槍枝,每次都只能跟他們買),常常有槍會卡彈,無法順利擊發。
「你們賣的槍都沒好貨;根據我們統計,你們賣的槍的擊發率,是從 0% ~ 100 % 平均分布,也就是說平均每買十把槍,只會有一把的擊發率在 90% 以上。」你向走私販抱怨著。
註 1:「擊發率」是指一把槍你拿來開一槍,子彈成功擊發的機率。這裡假設用同一把槍每次開槍的擊發率都相同。
註 2:「0% ~ 100 % 平均分布」的意思是,舉例來說,走私販有一批 1000 把槍的貨,如果去測每一把的擊發率,會發現 擊發率在 0% ~ 10% 約有100 把、10% ~ 20 % 也約有100把、……直到 90 % ~ 100% 的都是約有100把。(表示這批貨的品質很差!)
「好啦…大哥請息怒」 一位走私販好聲好氣地說。「要不這樣,這次你買回去之前,每把槍都讓你試射三發,你覺得滿意再買,如何?」
「好吧。」於是你就開始從一大堆的槍枝存貨中一把一把地試。
你的老大交代要買到 "好槍" (擊發率 90% 以上)。你盤算了一下,想說如果一把槍試射三發,即便只有一發失敗 (成功兩發),擊發率算下來都只有三分之二 (約 67%);所以你試槍的時候,都只留下 "三發試射都成功擊發" 的槍 (沒有連三發都成功的槍你就不要),最後總共挑了 1000 把槍。然後你就買下這些槍,拿回去交差了。
那麼,你買的這 1000 把槍中, 到底 "好槍" (擊發率 90% 以上) 約有幾把呢?
給個大概的數量就好,如 800~900、700~800、…等等。
(建議先憑直覺猜一下答案,然後再實際算算看。)
請會算的朋友們在答案公布前不要在留言板貼出算法哦~
猜答案則歡迎 XD
看答案
只有大概 350 把 而已。
順帶一提,如果要確保選購的槍枝,有九成數量的槍有 90% 以上擊發率,則試槍的時候每一把至少要試 21 發 (當然全都要成功才行)。
順帶一提,如果要確保選購的槍枝,有九成數量的槍有 90% 以上擊發率,則試槍的時候每一把至少要試 21 發 (當然全都要成功才行)。
解析
我要編輯原本的槍枝庫存,擊發率是 0~100% 平均分布。假設擊發率為 p ,則槍枝的統計分部圖如下:
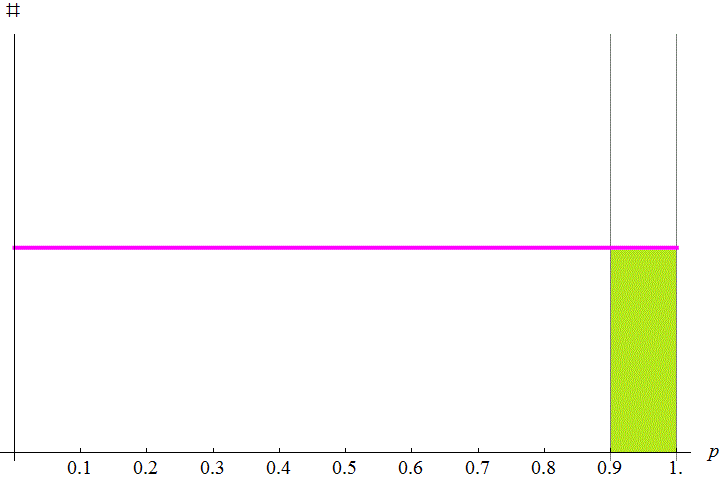
根據統計圖的概念,粉紅色線下方的面積就是槍枝的總數量。可以發現圖中 p > 0.9 的"好槍"數量 (綠色面積) 佔總數量 (粉色線下方的的面積) 的 1 - 0.9 = 0.1;這也就是說,如果你完全都不試槍就買了,你買到好槍的數量會佔總數的 10% (很合理吧)。
現在看看試射一發的情形。因為只會留下試槍有成功的槍,應該可以想見,擊發率高的槍較容易被留下來;而且,一把槍被留下來的機率會正比於他的擊發率 (例如:擊發率在 70~80% 之間的槍,試射一發後被留下的機率,應該會是擊發率在 35~40%的槍 的兩倍,這樣很合理。)。因此作圖時,分布就應該是 「正比於 p (擊發率)」的直線。如下:
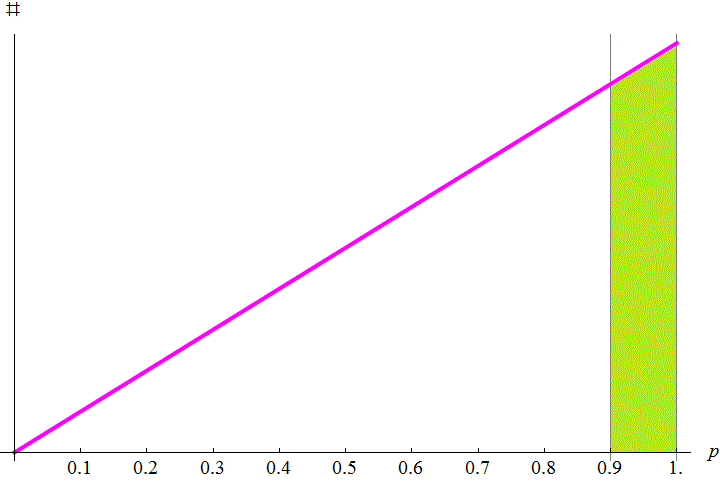
圖中粉色線是表示 正比與 p 的直線 (方程式即 y = ax ,a 是常數)。同樣,粉色線下方的面積就是槍枝總數。這時,"好槍"的部分 (綠色) 會佔總面積的 12 - 0.92 = 0.19 (用三角形面積公式 或積分都可以得知),也就是說好槍會佔 19%。
同理,試射三發的時候,留下槍枝的比率會正比於 p3 (每多試一次 就多正比於一次 擊發率),作圖如下:
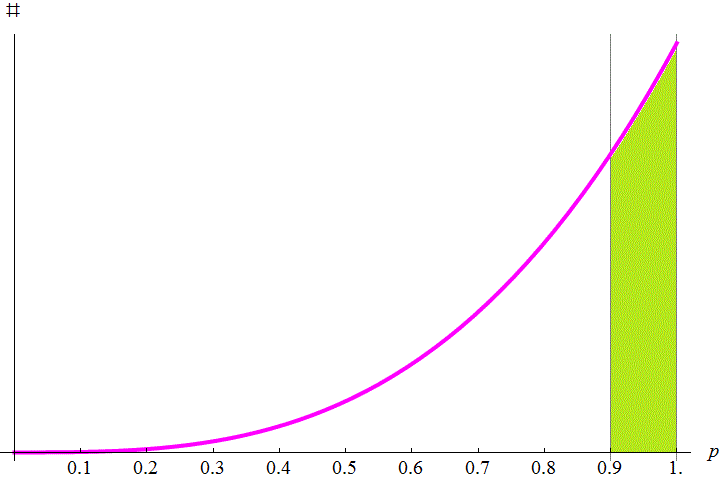
圖中粉色線是 正比於 p3 的圖 (方程式即 y = ax3 ,a 是常數)。一樣,好槍的比例就是算綠色面積佔粉色線以下總面積的多少。這裡要用到積分了,比例算法即是 14 - 0.94 = 1 - 0.6561 = 0.3439 ,約 34.4%。 (不會積分的朋友先暫時相信面積比是這樣算的吧。可以想成類比上一張圖,p 一次方的圖 底下面積比用 二次方相減;因此這裡 p 三次方的圖 底下面積比就用 四次方相減)
因此,1000 隻槍中,好槍只有 1000 × 34.4% = 344 把,大概 350 隻把左右。
另外,如果要買到數量有九成以上是好槍,假設需要試射 n 發,根據以上公式,好槍的比例是 1n+1 - 0.9 n+1 。令它要大於 0.9 ,可解得 n >= 21 ,即要試射 21 發。

根據統計圖的概念,粉紅色線下方的面積就是槍枝的總數量。可以發現圖中 p > 0.9 的"好槍"數量 (綠色面積) 佔總數量 (粉色線下方的的面積) 的 1 - 0.9 = 0.1;這也就是說,如果你完全都不試槍就買了,你買到好槍的數量會佔總數的 10% (很合理吧)。
現在看看試射一發的情形。因為只會留下試槍有成功的槍,應該可以想見,擊發率高的槍較容易被留下來;而且,一把槍被留下來的機率會正比於他的擊發率 (例如:擊發率在 70~80% 之間的槍,試射一發後被留下的機率,應該會是擊發率在 35~40%的槍 的兩倍,這樣很合理。)。因此作圖時,分布就應該是 「正比於 p (擊發率)」的直線。如下:

圖中粉色線是表示 正比與 p 的直線 (方程式即 y = ax ,a 是常數)。同樣,粉色線下方的面積就是槍枝總數。這時,"好槍"的部分 (綠色) 會佔總面積的 12 - 0.92 = 0.19 (用三角形面積公式 或積分都可以得知),也就是說好槍會佔 19%。
同理,試射三發的時候,留下槍枝的比率會正比於 p3 (每多試一次 就多正比於一次 擊發率),作圖如下:

圖中粉色線是 正比於 p3 的圖 (方程式即 y = ax3 ,a 是常數)。一樣,好槍的比例就是算綠色面積佔粉色線以下總面積的多少。這裡要用到積分了,比例算法即是 14 - 0.94 = 1 - 0.6561 = 0.3439 ,約 34.4%。 (不會積分的朋友先暫時相信面積比是這樣算的吧。可以想成類比上一張圖,p 一次方的圖 底下面積比用 二次方相減;因此這裡 p 三次方的圖 底下面積比就用 四次方相減)
因此,1000 隻槍中,好槍只有 1000 × 34.4% = 344 把,大概 350 隻把左右。
另外,如果要買到數量有九成以上是好槍,假設需要試射 n 發,根據以上公式,好槍的比例是 1n+1 - 0.9 n+1 。令它要大於 0.9 ,可解得 n >= 21 ,即要試射 21 發。
7,156
上一道精選數學謎題
下一道精選數學謎題
 有一塊草坪,形狀是正三角形的,三個頂點處都各有一個樁子。草坪中 (不是正中央) 插了一枝旗子。
有個...
有一塊草坪,形狀是正三角形的,三個頂點處都各有一個樁子。草坪中 (不是正中央) 插了一枝旗子。
有個...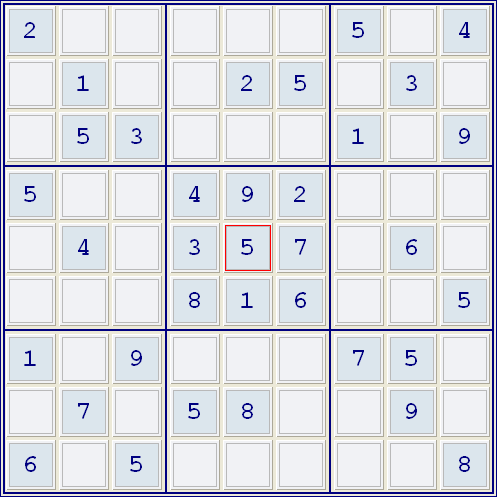 數獨遊戲中,一開始給的數字越多,就會越容易解嗎?試試看以下的題目吧。
請完成以下數獨:
解出的朋友,...
數獨遊戲中,一開始給的數字越多,就會越容易解嗎?試試看以下的題目吧。
請完成以下數獨:
解出的朋友,... F 先生有個奇怪的癖好,
他固定在星期五說謊,而且說的每一句都是謊話,
而其它日子他都是說實話的;
...
F 先生有個奇怪的癖好,
他固定在星期五說謊,而且說的每一句都是謊話,
而其它日子他都是說實話的;
...