上一道精選數學謎題
下一道精選數學謎題
費氏數列前十項之和數學謎題
答對率:67%
小楷問小治:『你知道費氏數列嗎?』
小治:『知道啊,數列的前兩個數是0, 1,
然後後面每個數都是前兩項相加之和。』
小楷:『看來你數學課有認真聽嘛,那你現在隨便選兩個數,
然後繼續把它用費氏數列的規則寫成十項。』
小治心想:『(那我選今天的日期:7, 16)』
然後在紙上計算出了十項:7, 16, 23, 39, 62, 101, 163, 264, 427, 691
小楷完全沒在看小治列數列,等他列完十項後才拿起紙來看了一眼,
不到三秒的時間,就說:『這十項加起來是1793。』
小治:『最好是,你從小就沒學過心算,哪會算這麼快!』
沒想到,小治一驗算,居然真的是1793沒錯,
後來他們試了好幾輪,
小治不管怎麼選數字,小楷都能在看一眼那個數列之後極快地回答總和,
你知道小楷是怎麼辦到的嗎?
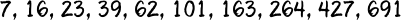
看答案
費氏數列前十項的總和剛好等於第七項的11倍。
而一個數字的11倍是很容易計算的,
用直式展開相乘的時候你會發現只要把那個數字寫兩次,
第二次往右偏移一位數,然後兩排數字相加即可,像163的11倍:
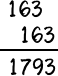
至於「費氏數列前十項的總和剛好等於第七項的11倍」這個規律,
就留給大家有興趣的人去證明啦!
解析
我要編輯作者:9876543210(ABC) | 歷史版本
設a為首項,b為次項。數列的前十項便是:
a,b,a+b,a+2b,2a+3b,3a+5b,5a+8b,8a+13b,13a+21b,21a+34b
而它們的總和=55a+88b=11(5a+8b)=11乘以數列的第七項
a,b,a+b,a+2b,2a+3b,3a+5b,5a+8b,8a+13b,13a+21b,21a+34b
而它們的總和=55a+88b=11(5a+8b)=11乘以數列的第七項
11,779
上一道精選數學謎題
下一道精選數學謎題
 在某次駕駛當中,巴士司機因為切線的問題和一名計程車司機起了爭執。
當巴士到達巴士站停下後,計程車司機...
在某次駕駛當中,巴士司機因為切線的問題和一名計程車司機起了爭執。
當巴士到達巴士站停下後,計程車司機...