三人運動會數學謎題
乍看之下解不出來的題目,其實是有解的喔!快來挑戰看看吧!
小金、小楷、小治舉行了三人運動會,比了好幾種比賽,
並規定每場比賽的第一名可得a分、第二名可得b分、第三名可得c分,
計分都是整數,且a>b>c>0;
第一場比的是賽跑,小治拔得頭籌;
全部比完後,沒有一場有平手的狀況,
小金的總積分是22分,小楷、小治的總積分各都是9分;
請問,賽跑第二名的人是誰?這次運動會總共舉辦了幾場比賽?

賽跑第二名的人是小金,總共比了5場比賽。
解析
我要編輯三人得的總分是22+9+9=40分,所以每場三名的分數加總(a+b+c)必定是40的因數,
可能的有:1、2、4、5、8、10、20、40;
因為a>b>c>0,所以a+b+c至少要是6,
可能性剩下:8、10、20、40;
如果a+b+c=40,則只有比1場,小楷小治不可能同分,因此不可能是40
可能性剩下:8、10、20;
如果a+b+c=20,則比了2場,第一名至少要超過20/3=6.7分,所以小治不可能兩場都第一,
小治第一名那場得a分,非第一名那場得(9-a)分,
則小治沒得過的那個名次(可能為第二或第三名)為20-a-(9-a)=11分,
已知第一名小於9分,所以第二或三名為11分是不合題意的,
因此a+b+c=20的狀況不可能發生,
可能性剩下:8、10;
如果a+b+c=10,則比了4場,第一名至少要超過10/3=3.3分,
又,每場小治至少要得1分,所以第一名那場小治至多得9-1x(4-1)=6分,
由以上兩點可知4≦a≦6,
列出(a,b,c)可能的組合為:(5,3,2)、(5,4,1)、(6,3,1)
其中前兩組都不可能讓小治得到9分,
而(6,3,1)當小治得了1次第一,其他3次都第三的時候可以符合9分,
但這樣一來小楷就至少有3次第二名,就已經得了3x3=9分,第4場就不可能有分數了,因此也不符合;
可能性剩下:8;≦6,
≦6,
當a+b+c=8,則比了5場,第一名至少要超過8/3=2.6分,
又,每場小治至少要得1分,所以第一名那場小治至多得9-1x(5-1)=5分,
由以上兩點可知3≦a≦5,
列出(a,b,c)可能的組合為:(4,3,1)、(5,2,1)
其中(4,3,1)不可能讓小治得到9分,
所以只可能是a=5, b=2, c=1
由a,b,c跟三人的總分可以推得:
- 小治得到9分:賽跑第一,其他4場第三
- 小楷得到9分:賽跑第三,其他4場第二
- 小金得到22分:賽跑第二,其他4場第一
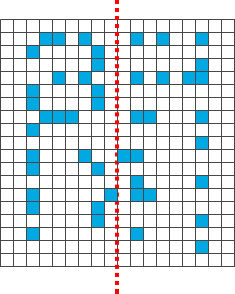 下面的方格中,把每個藍色格子沿紅色對稱軸鏡射到另一邊,
會形成一個左右對稱的中文字,
不用紙筆輔助,...
下面的方格中,把每個藍色格子沿紅色對稱軸鏡射到另一邊,
會形成一個左右對稱的中文字,
不用紙筆輔助,... 劇情承接上題。
「不錯不錯!」張三稱讚,同時將李四移動的那三根火柴擺回原位。
「咦?還有一道題目啊?...
劇情承接上題。
「不錯不錯!」張三稱讚,同時將李四移動的那三根火柴擺回原位。
「咦?還有一道題目啊?...