上一道精選找規律謎題
下一道精選找規律謎題
冷門的數列找規律謎題
答對率:59%
1,1,2,3,5,8,13,21,34....
但其實還有許許多多如費氏數列一般,有著獨特規律性的數列
你能嘗試解開以下幾個數列的祕密嗎?
1)
1,1,1,2,2,3,4,5,7,9,12,16,21,28,?,...
2)
6,?,496,8128,33550336,8589869056,....
3)
1,2,3,4,6,8,11,13,16,18,26,?,......
4)
4, 6, 9, 10, 14, 15, 21, 22, 25, ?
看答案
1)
37
2)
28
3)
28
4)
26
37
2)
28
3)
28
4)
26
解析
我要編輯作者:ms0592138(小分/阿分/繽紛) | 歷史版本
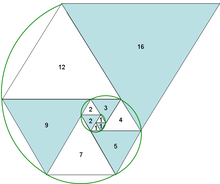
1)巴都萬數列(Padovan Sequence)
巴都萬數列是由起始數值P_0=P_1=P_2=1,及遞歸關係P_n-3+P_n-2=P_n定義。
簡單來說,就是前三項都是1,第4項是第1、2項和,第5項是第2、3項和...第n項是第n-3、n-2項和
巴都萬數列如費氏數列,有幾何上的應用,不同於費氏數列,巴都萬數列是以正三角形的排列組合出的螺旋狀。
如圖:(圖中標示的數字為邊長)
參考資料:
https://zh.wikipedia.org/wiki/%E5%B7%B4%E9%83%BD%E8%90%AC%E6%95%B8%E5%88%97
https://oeis.org/A000931
2)完全數
完全數是一種特殊的自然數,完全數的特性為:除了本身以外的正因數和恰等於它本身。
例如6=1+2+3,28=1+2+4+7+14
古希臘科學家歐幾里得透過表達式2n-1(2n-1)發現前四個完全數。
一個偶數是完全數的充分必要條件為其可表為2n-1(2n-1)且(2n-1)為質數。此事實的充分性由歐幾里得證明,而必要性則由歐拉所證明。
參考資料
https://zh.wikipedia.org/wiki/%E5%AE%8C%E5%85%A8%E6%95%B0
3)烏拉姆數列
烏拉姆數列,從前兩項為1、2,之後對於第n項(n>2),Un為最小而又能剛好以一種方法表達成之前其中兩個相異項的和。
例如3=1+2,所以3在此數列中,U3=3
又4=1+3(注意2+2不算在其中),U4=4
但5=1+4=2+3,有兩種表示方法,故5不在此數列中。
參考資料:
https://zh.wikipedia.org/wiki/%E7%83%8F%E6%8B%89%E5%A7%86%E6%95%B8%E5%88%97
https://oeis.org/A002858
4)半質數
兩個質數相乘的乘積稱為半質數。半質數在密碼學和數論中非常有用,最顯著的例子是密碼學中的公鑰(例如RSA加密演算法)和隨機數發生器。主要的基本原理是利用這類數難以進行因數分解的特性。舉例來說,小的半質數如35可輕易分解為5x7,但較大的半質數如32111(=163x197)就需要較多的時間進行分解,RSA加密演算法中有一個稱為RSA-2048的半質數,有2,048位元,十進位有617位,RSA曾公開懸賞200,000美元,給予成功將RSA-2048因數分解的人,迄2007年活動終止,未有人挑戰成功領取懸賞。
參考資料
https://zh.wikipedia.org/wiki/%E5%8D%8A%E7%B4%A0%E6%95%B0
巴都萬數列是由起始數值P_0=P_1=P_2=1,及遞歸關係P_n-3+P_n-2=P_n定義。
簡單來說,就是前三項都是1,第4項是第1、2項和,第5項是第2、3項和...第n項是第n-3、n-2項和
巴都萬數列如費氏數列,有幾何上的應用,不同於費氏數列,巴都萬數列是以正三角形的排列組合出的螺旋狀。
如圖:(圖中標示的數字為邊長)

參考資料:
https://zh.wikipedia.org/wiki/%E5%B7%B4%E9%83%BD%E8%90%AC%E6%95%B8%E5%88%97
https://oeis.org/A000931
2)完全數
完全數是一種特殊的自然數,完全數的特性為:除了本身以外的正因數和恰等於它本身。
例如6=1+2+3,28=1+2+4+7+14
古希臘科學家歐幾里得透過表達式2n-1(2n-1)發現前四個完全數。
一個偶數是完全數的充分必要條件為其可表為2n-1(2n-1)且(2n-1)為質數。此事實的充分性由歐幾里得證明,而必要性則由歐拉所證明。
參考資料
https://zh.wikipedia.org/wiki/%E5%AE%8C%E5%85%A8%E6%95%B0
3)烏拉姆數列
烏拉姆數列,從前兩項為1、2,之後對於第n項(n>2),Un為最小而又能剛好以一種方法表達成之前其中兩個相異項的和。
例如3=1+2,所以3在此數列中,U3=3
又4=1+3(注意2+2不算在其中),U4=4
但5=1+4=2+3,有兩種表示方法,故5不在此數列中。
參考資料:
https://zh.wikipedia.org/wiki/%E7%83%8F%E6%8B%89%E5%A7%86%E6%95%B8%E5%88%97
https://oeis.org/A002858
4)半質數
兩個質數相乘的乘積稱為半質數。半質數在密碼學和數論中非常有用,最顯著的例子是密碼學中的公鑰(例如RSA加密演算法)和隨機數發生器。主要的基本原理是利用這類數難以進行因數分解的特性。舉例來說,小的半質數如35可輕易分解為5x7,但較大的半質數如32111(=163x197)就需要較多的時間進行分解,RSA加密演算法中有一個稱為RSA-2048的半質數,有2,048位元,十進位有617位,RSA曾公開懸賞200,000美元,給予成功將RSA-2048因數分解的人,迄2007年活動終止,未有人挑戰成功領取懸賞。
參考資料
https://zh.wikipedia.org/wiki/%E5%8D%8A%E7%B4%A0%E6%95%B0
13,143
上一道精選找規律謎題
下一道精選找規律謎題