上一道精選空間概念謎題
下一道精選空間概念謎題
正立方體的最大切面空間概念謎題
答對率:82%
有一個正立方體,
從不同角度直切一刀可以形成多種不同的橫切面,
請問,怎麼切可以切出面積最大的橫切面呢?
看答案
如下圖從頂面的對角線直直往下切到底:
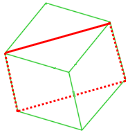
(註:原提供之正六邊形切法並非正解,感謝網友反映修正)
解析
我要編輯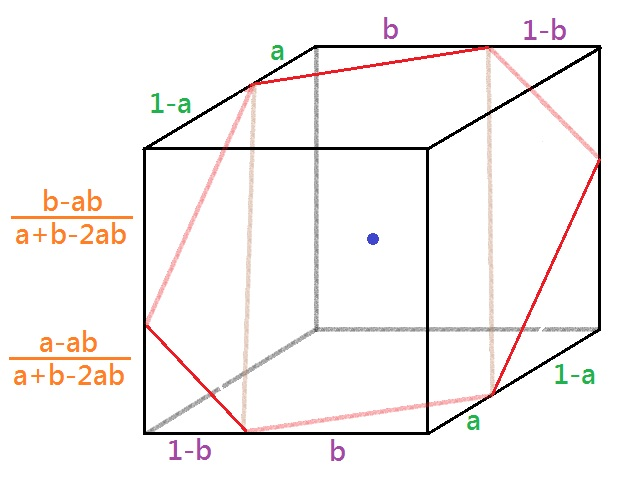
這裡只考慮截面有過正方體中心的情形。如上圖,正方體邊長為 1 ,紅色區為一個過方體中心的截面,假設截於兩個邊到一個頂點的距離分別為 a 與 b (隨著截面不同而改變)。那麼由於對稱性 (因為截面過中心),在對面的位置的截距也是 a 與 b ;而由於截面為一平面,故截於第三條邊的截點會把邊分成 (a-ab)/(a+b-2ab) 與 (b-ab)/(a+b-2ab)。
這樣,就可以計算截面 (六邊形) 的面積。如圖,將六邊形切成兩個全等的三角形和一個平行四邊形。
兩個三角形的面積 = √2 × (1-a)(1-b) × √( a2 + ab + b2 -2a2b -2ab2 + 2a2b2 ) / (a + b - 2ab)
平行四邊形的面積 = √( a2 + b2 + (a + b - 2ab)2 )
將以上兩者相加即為六邊形的面積。 (以上計算皆可用高中數學的空間向量來計算;例如,解平面方程、用向量外積來算面積等等…)
這個面積的式子很複雜,就交給電腦吧…。圖形如下:
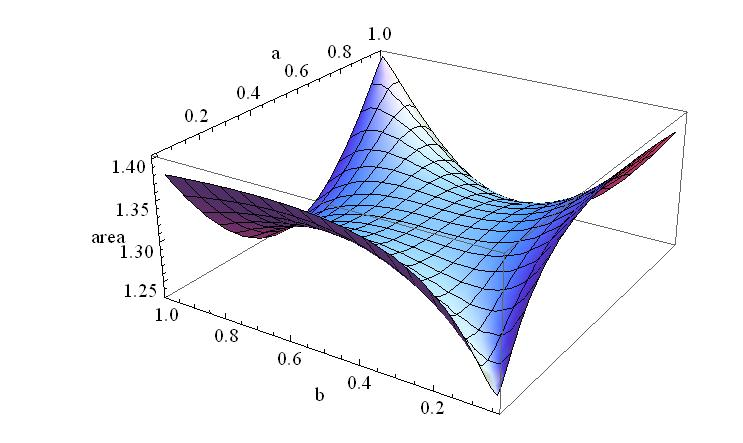
這是三維的圖,鉛直方向的軸代表截面積大小,另兩個軸代表 a 和 b 的值 (介於 0 和 1 之間)。可以看出有三組 (a,b) 讓截面積最大 (面積是 √2 ≈1.41 ) ,分別是 (a,b) = (0,1)、(1,0)、(1,1),而這三種都對應到 bbbnnn 大所解的長方形。(註: 如果真的把 (a,b) = (0,1)、(1,0)、(1,1) 代入以上的截面積式子,會出現分母為 0 的情形;但是從上圖中截面積隨著 a、b 變化的趨式,還是可以知道以上三組是截面積最大的。)
因此如果截面要過正方體中心,那最大就是沿正方形對角線垂直切下去的長方形了。至於是不是所有截面最大的?我覺得是,但在此不討論了。或許有朋友可以說明 不過中心的截面 的情形。
P.S. 各位可以想想,過中心的截面,面積「最小」的是要怎樣切。(若要求截面過相鄰兩邊則答案可由上圖得到,否則就是平行任一表面截出邊長為 1 的正方形)。
11,486
上一道精選空間概念謎題
下一道精選空間概念謎題
 有兩名犯人,
一名犯人是偽造文書罪,他被判要關兩年;
另一名犯人是強盜殺人罪,但他卻只要被關兩個星期...
有兩名犯人,
一名犯人是偽造文書罪,他被判要關兩年;
另一名犯人是強盜殺人罪,但他卻只要被關兩個星期... 明天是甜蜜的情人節,但今天是恐怖的十三號星期五喔!來解個應景的謎題吧~
十三號星期五在國外被視為不吉...
明天是甜蜜的情人節,但今天是恐怖的十三號星期五喔!來解個應景的謎題吧~
十三號星期五在國外被視為不吉... 有幾名啦啦隊員正在排練隊形,
他們想排出『任兩位隊員之間的距離都是相等的』的隊形,
比如說:三個隊員...
有幾名啦啦隊員正在排練隊形,
他們想排出『任兩位隊員之間的距離都是相等的』的隊形,
比如說:三個隊員... 在方塊底部角落有一隻非常飢餓的毛毛蟲,
在方塊頂端角落有一片好吃的樹葉,
位置如下圖:
請幫這隻毛毛...
在方塊底部角落有一隻非常飢餓的毛毛蟲,
在方塊頂端角落有一片好吃的樹葉,
位置如下圖:
請幫這隻毛毛...