上一道精選數學謎題
下一道精選數學謎題
數字差金字塔數學謎題
答對率:85%
數字差金字塔的規則是這樣的:
每一個上面的數字,都要等於它下面兩個數字的差,
且金字塔內不能有重複的數字,
如下圖範例,3=5-2, 5=6-1, 2=6-4
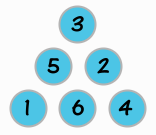
那麼,
你能夠把1~10這十個數字也堆出一個數字差金字塔來嗎?
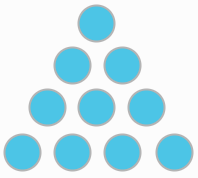
看答案
答案有很多種,下面是其中之一:
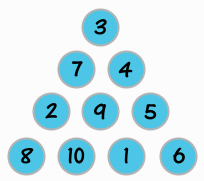
解析
我要編輯首先,我們將這十個圈圈分成四類: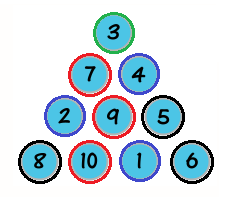
綠圈─最上面的圈圈
紅圈─綠圈或紅圈底下兩個數字中比較大的那個,在這有3個紅圈
藍圈─綠圈或紅圈底下兩個數字中比較小的那個,在這有3個籃圈
黑圈─剩下的圈圈,也會有3個
如果將腦補給的答案依此方法分類的話,就會像右圖:
(註:以下所提的圈圈主要都是指在該圈圈內的數字)
那麼,推論要開始了!
I. 10一定會在最下面
因為任兩個數的差不會大於10-1=9,故如果10不在最下面的話,10下面不會有符合條件的數字組。
所以10一定要在最下面
II. 任意一個紅圈為綠圈加上所有不比該紅圈下面的藍圈和
由紅圈的定義,可知在一個紅-紅-藍(或綠-紅-藍)的小三角形內(正的三角形,不是倒的三角形),下面的紅圈-藍圈=上面的紅圈(或紅圈-藍圈=綠圈),即下面的紅圈=上面的紅圈+藍圈(或紅圈=綠圈+藍圈)。
因此將紅圈慢慢拆開,會得到所有不比該紅圈還要下面的藍圈和綠圈。
以腦補的答案為例:9=2+7=2+4+3
III. 所有藍圈和綠圈絕對會是1~4;最底下的紅圈只可以為10
由II可知,所有藍圈和綠圈的和為最底下的紅圈,則該紅圈>=1+2+3+4=10。
但我們最大的數字只有10,故最底下的紅圈只可以為10。
而所有藍圈和綠圈就會是1~4。
相對的,1~4只能填到藍圈和綠圈內;10只能填到最底下的紅圈。
IV. 最上面的綠圈和藍圈只能為(1,4) (2,3) (2,4) (3,4)其中一種
如果最上面的綠圈和藍圈為(1,2)的話,則藍色旁邊的紅色會是3。
但由III可知3只能填入藍圈或綠圈,故不合。
同理(1,3)也不行。
V. 請看敘述吧...
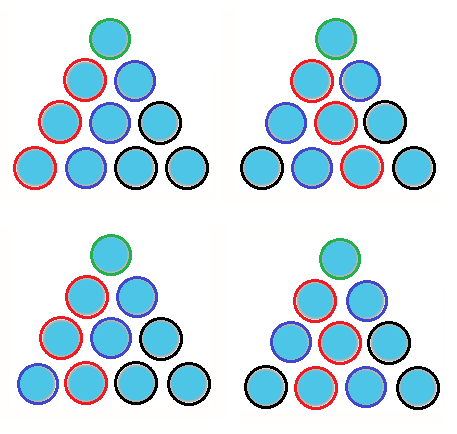
如果將左右對稱視為同種,則圈圈顏色的排列方法只有右邊四種。
如果是左邊兩種的話,則會在右下角形成一個二階的小數字差金字塔。
由III可知填入的數須從5~9去取,由II可知其中一個要是另外兩個的和。
但是任意兩個數的和>=5+6=11,故不合。
所以排列方法只能為右邊兩種。
大致上就是這些了,然後用這些條件去慢慢找,就可以找出以下解答:
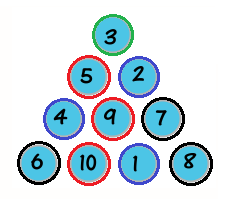
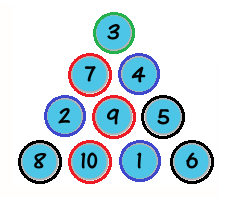
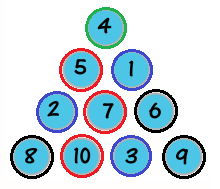
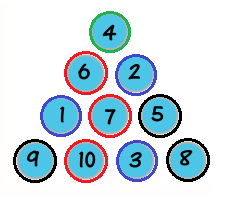
看起來紅色圈的排法也只有一種,雖然這是可以證明的,但我就不多詳述了。
另外也還有兩個條件沒有提到,雖然在這裡是不太需要,但也是一個好的條件
VI. 在同一層中,藍圈是那一層最小的數
由前面所提可知每一層僅有一個藍圈。
而藍圈的組成為1~4的其中三個數,這意味著不論是紅圈還是黑圈,都會比任何一個藍圈大。
且藍圈所在的層也只會有紅圈或黑圈。
所以藍圈會是該層之中最小的數字。
VII. 在同一層中,紅圈是那一層最大的數
這裡我們採數學歸納法。
其中最底層為第一層,每往上一層加1。
a. 10為第一層中最大的數(10也是整個三角形中最大的數)。
b. 如果第k層中紅圈為第k層中最大的數,那麼第k+1層也會是第k+1層中最大的數。
由VI 可知第k層的藍圈為第k層中最小的數。
而第k+1層的數理論上最大為第k層中的紅圈減去第k層中的藍圈。
而由定義可知此數為第k+1層的紅圈。
由此可知第k+1層的紅圈為第k+1層的最大的數。
而由a和b可知所有紅圈為該層中的最大的數。

綠圈─最上面的圈圈
紅圈─綠圈或紅圈底下兩個數字中比較大的那個,在這有3個紅圈
藍圈─綠圈或紅圈底下兩個數字中比較小的那個,在這有3個籃圈
黑圈─剩下的圈圈,也會有3個
如果將腦補給的答案依此方法分類的話,就會像右圖:
(註:以下所提的圈圈主要都是指在該圈圈內的數字)
那麼,推論要開始了!
I. 10一定會在最下面
因為任兩個數的差不會大於10-1=9,故如果10不在最下面的話,10下面不會有符合條件的數字組。
所以10一定要在最下面
II. 任意一個紅圈為綠圈加上所有不比該紅圈下面的藍圈和
由紅圈的定義,可知在一個紅-紅-藍(或綠-紅-藍)的小三角形內(正的三角形,不是倒的三角形),下面的紅圈-藍圈=上面的紅圈(或紅圈-藍圈=綠圈),即下面的紅圈=上面的紅圈+藍圈(或紅圈=綠圈+藍圈)。
因此將紅圈慢慢拆開,會得到所有不比該紅圈還要下面的藍圈和綠圈。
以腦補的答案為例:9=2+7=2+4+3
III. 所有藍圈和綠圈絕對會是1~4;最底下的紅圈只可以為10
由II可知,所有藍圈和綠圈的和為最底下的紅圈,則該紅圈>=1+2+3+4=10。
但我們最大的數字只有10,故最底下的紅圈只可以為10。
而所有藍圈和綠圈就會是1~4。
相對的,1~4只能填到藍圈和綠圈內;10只能填到最底下的紅圈。
IV. 最上面的綠圈和藍圈只能為(1,4) (2,3) (2,4) (3,4)其中一種
如果最上面的綠圈和藍圈為(1,2)的話,則藍色旁邊的紅色會是3。
但由III可知3只能填入藍圈或綠圈,故不合。
同理(1,3)也不行。

V. 請看敘述吧...
如果將左右對稱視為同種,則圈圈顏色的排列方法只有右邊四種。
如果是左邊兩種的話,則會在右下角形成一個二階的小數字差金字塔。
由III可知填入的數須從5~9去取,由II可知其中一個要是另外兩個的和。
但是任意兩個數的和>=5+6=11,故不合。
所以排列方法只能為右邊兩種。
大致上就是這些了,然後用這些條件去慢慢找,就可以找出以下解答:




看起來紅色圈的排法也只有一種,雖然這是可以證明的,但我就不多詳述了。
另外也還有兩個條件沒有提到,雖然在這裡是不太需要,但也是一個好的條件
VI. 在同一層中,藍圈是那一層最小的數
由前面所提可知每一層僅有一個藍圈。
而藍圈的組成為1~4的其中三個數,這意味著不論是紅圈還是黑圈,都會比任何一個藍圈大。
且藍圈所在的層也只會有紅圈或黑圈。
所以藍圈會是該層之中最小的數字。
VII. 在同一層中,紅圈是那一層最大的數
這裡我們採數學歸納法。
其中最底層為第一層,每往上一層加1。
a. 10為第一層中最大的數(10也是整個三角形中最大的數)。
b. 如果第k層中紅圈為第k層中最大的數,那麼第k+1層也會是第k+1層中最大的數。
由VI 可知第k層的藍圈為第k層中最小的數。
而第k+1層的數理論上最大為第k層中的紅圈減去第k層中的藍圈。
而由定義可知此數為第k+1層的紅圈。
由此可知第k+1層的紅圈為第k+1層的最大的數。
而由a和b可知所有紅圈為該層中的最大的數。
17,554
上一道精選數學謎題
下一道精選數學謎題
 一般足球是用正五邊形的黑色皮塊跟正六邊形的白色皮塊縫製而成的(如下圖),
已知要縫製一顆足球要用12...
一般足球是用正五邊形的黑色皮塊跟正六邊形的白色皮塊縫製而成的(如下圖),
已知要縫製一顆足球要用12... 只用眼睛看,下面哪一顆星星離中間的地球最遠?
哪一顆離地球最近?
只用眼睛看,下面哪一顆星星離中間的地球最遠?
哪一顆離地球最近?
 有聲有色。
(射一字)
有聲有色。
(射一字)
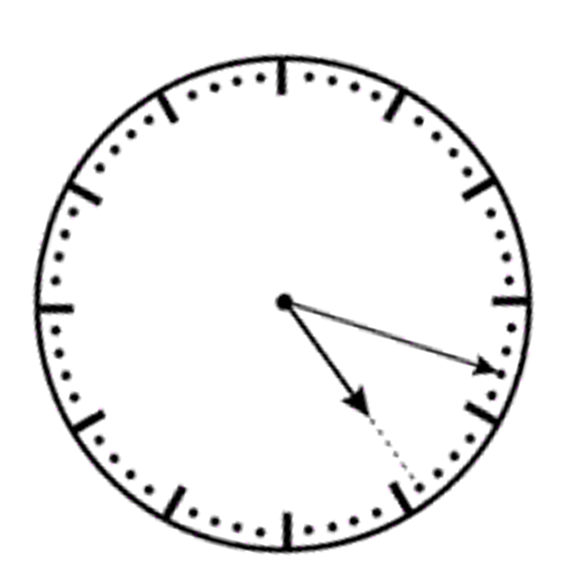 96基測第一次第33題
稍微修改一下問題,有一個沒數字的時鐘不小心倒在地上了,請問幾點幾分?
96基測第一次第33題
稍微修改一下問題,有一個沒數字的時鐘不小心倒在地上了,請問幾點幾分?