上一道數學謎題
下一道數學謎題
乘法abc數學謎題
答對率:67%
- 乘法表
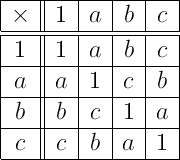
- a,b,c和實數的加法符合交換律
- 即對任意實數x都有a+x=x+a,b+x=x+b,c+x=x+c
- a,b,c和實數的加法符合結合律
- 即對任意數x,y,z(包括a,b,c)都有(x+y)+z=x+(y+z)
- a,b,c和實數的乘法符合交換律
- 即對任意實數x都有a*x=x*a,b*x=x*b,c*x=x*c
- a,b,c和實數的乘法符合結合律
- 即對任意數x,y,z(包括a,b,c)都有(x*y)*z=x*(y*z)
- a,b,c和實數的加法和乘法符合分配律
- 即對任意實數w,x,y,z(包括a,b,c)都有(w+x)*(y+z)=w*y+w*z+x*y+x*z
- a+(-a)=b+(-b)=c+(-c)=0
- -a=-1*a,-b=-1*b,-c=-1*c
及(1+a+b+c)(1+a+b-c)(1+a-b+c)(1-a+b+c)(1-a+b-c)(1+a-b-c)(1-a-b+c)(1-a-b-c)
看答案
(1+a+b+c)2013=42012(1+a+b+c)
(1+a+b+c)(1+a+b-c)(1+a-b+c)(1-a+b+c)(1-a+b-c)(1+a-b-c)(1-a-b+c)(1-a-b-c)=0
(1+a+b+c)(1+a+b-c)(1+a-b+c)(1-a+b+c)(1-a+b-c)(1+a-b-c)(1-a-b+c)(1-a-b-c)=0
解析
我要編輯作者:climbn1246(climbn) | 歷史版本
因為(1+a+b+c)(1+a+b+c)
=1+a+b+c+a+1+c+b+b+c+1+a+c+b+a+1
=4(1+a+b+c)
(1+a+b+c)2013=4(1+a+b+c)2012=42(1+a+b+c)2011=...=42012(1+a+b+c)
(1-a+b-c)(1+a-b-c)=1+a-b-c-a-1+c+b+b+c-1-a-c-b+1+a=0
(1+a+b+c)(1+a+b-c)(1+a-b+c)(1-a+b+c)(1-a+b-c)(1+a-b-c)(1-a-b+c)(1-a-b-c)
=(1+a+b+c)(1+a+b-c)(1+a-b+c)(1-a+b+c)0(1-a-b+c)(1-a-b-c)
=0
=1+a+b+c+a+1+c+b+b+c+1+a+c+b+a+1
=4(1+a+b+c)
(1+a+b+c)2013=4(1+a+b+c)2012=42(1+a+b+c)2011=...=42012(1+a+b+c)
(1-a+b-c)(1+a-b-c)=1+a-b-c-a-1+c+b+b+c-1-a-c-b+1+a=0
(1+a+b+c)(1+a+b-c)(1+a-b+c)(1-a+b+c)(1-a+b-c)(1+a-b-c)(1-a-b+c)(1-a-b-c)
=(1+a+b+c)(1+a+b-c)(1+a-b+c)(1-a+b+c)0(1-a-b+c)(1-a-b-c)
=0
4,745
上一道數學謎題
下一道數學謎題
 新年期間應該很多人都有買樂透彩券吧? 今天的題目再來應景一下,是真實統計數字喔~
台北銀行曾統計一億...
新年期間應該很多人都有買樂透彩券吧? 今天的題目再來應景一下,是真實統計數字喔~
台北銀行曾統計一億... 小金去美國玩,租了一輛六輪的露營車想要環遊美國,
整趟旅程預計要走11.5萬公里,非常遙遠,
而每顆...
小金去美國玩,租了一輛六輪的露營車想要環遊美國,
整趟旅程預計要走11.5萬公里,非常遙遠,
而每顆...