上一道其他謎題
下一道其他謎題
鋪設磁磚(五)其他謎題
答對率:60%
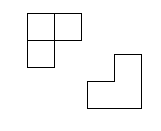
三方塊中有兩種, I 和 L ,今天我們會用到的是L。
一般來講,我們可以很簡單的將兩個 L 組成一個2x3的矩形。
並且可以用這個矩形去排更多的矩形。
但這些矩形都有個共通點:至少有一邊會是偶數的長度。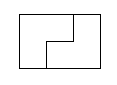
那請問,是否有辦法用這些 L 來鋪任意奇數長寬的矩形,或者是可以鋪那些矩形?
小知識:N方塊指的是總共用N個單位正方形鋪的圖形,其中一方塊只有一個;二方塊也只有一個;三方塊有兩個(I:一長條;L:你知道的);四方塊有五個( I L N O T);五方塊有12個(F I L M或W N P T U V X Y Z);六方塊...你自己算吧。
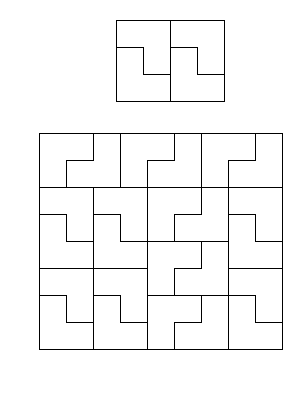
一般來講,我們可以很簡單的將兩個 L 組成一個2x3的矩形。
並且可以用這個矩形去排更多的矩形。
但這些矩形都有個共通點:至少有一邊會是偶數的長度。

那請問,是否有辦法用這些 L 來鋪任意奇數長寬的矩形,或者是可以鋪那些矩形?
小知識:N方塊指的是總共用N個單位正方形鋪的圖形,其中一方塊只有一個;二方塊也只有一個;三方塊有兩個(I:一長條;L:你知道的);四方塊有五個( I L N O T);五方塊有12個(F I L M或W N P T U V X Y Z);六方塊...你自己算吧。

看答案
凡可以蓋過5x9面積、其中一邊為3的倍數的所有符合條件的矩形都可以。
解析
我要編輯先只看比較短的一邊
如果長度為1......你說呢?
如果長度為3,那另外一邊一定是偶數,請大家自行想像。
所以我們討論5*5以上的矩形
當然了,因為每個零件都是3個方塊
所以至少要有一邊是3的倍數
因此我們將這個矩形重新分為兩種邊長:3的倍數和任意奇數
3的倍數這邊因為要求必須是奇數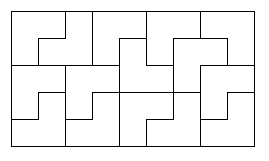
如果長度為1......你說呢?
如果長度為3,那另外一邊一定是偶數,請大家自行想像。
所以我們討論5*5以上的矩形
當然了,因為每個零件都是3個方塊
所以至少要有一邊是3的倍數
因此我們將這個矩形重新分為兩種邊長:3的倍數和任意奇數
3的倍數這邊因為要求必須是奇數

所以最小的就是9
而任意奇數這邊可以從5開始
而任意奇數這邊可以從5開始
所以我們先給出一個5*9的矩形,如右圖
接著,如果任意奇數的邊需要增加的話
每次需增加兩個單位
而兩個單位寬的長方形是很好做的,這點也給大家自行想像嚕
接著是3的倍數的邊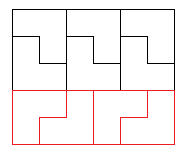
因為要求皆為奇數
所以一次加必須加6
於是乎,只要給出5*6的長方形,剩下的向上面一樣增加寬度就可以了
由此可見,凡能蓋過5*9的長方形、其中一邊為3的倍數的所有符合條件的長方形都可以被排出。
延伸問題:(不提供解答)
如果今天是3個1*1*1的單位立方體擺成的L狀立體作排列,那麼請問可以排哪些長方體呢?
接著,如果任意奇數的邊需要增加的話
每次需增加兩個單位
而兩個單位寬的長方形是很好做的,這點也給大家自行想像嚕
接著是3的倍數的邊

因為要求皆為奇數
所以一次加必須加6
於是乎,只要給出5*6的長方形,剩下的向上面一樣增加寬度就可以了
由此可見,凡能蓋過5*9的長方形、其中一邊為3的倍數的所有符合條件的長方形都可以被排出。
延伸問題:(不提供解答)
如果今天是3個1*1*1的單位立方體擺成的L狀立體作排列,那麼請問可以排哪些長方體呢?
4,145
上一道其他謎題
下一道其他謎題
 有一座半徑50公尺的圓形湖泊,
周圍寸草不生,只有湖泊正中央的小島上長了一顆椰子樹;
小金站在湖岸,...
有一座半徑50公尺的圓形湖泊,
周圍寸草不生,只有湖泊正中央的小島上長了一顆椰子樹;
小金站在湖岸,...