上一道精選移動成立謎題
下一道精選移動成立謎題
不排成正方形的40根火柴移動成立謎題
答對率:75%
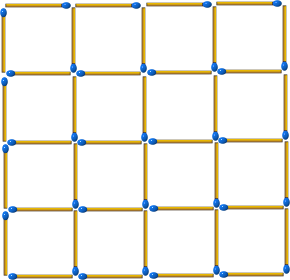
下面是用40根火柴棒排成的4X4正方形,
你能移走最少幾根火柴棒,使得圖中完全不會顯示出正方形呢?
(註:邊長1根、2根、3根、4根火柴的都算)
看答案
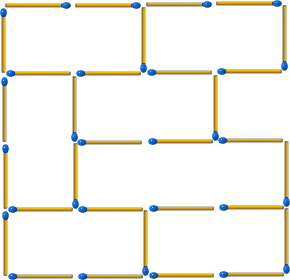
9根。
解析
我要編輯一種參考方法如下:
如何證明9根一定是最少呢?我們可以試著分析有沒有可能只移除8根火柴棒。
觀察如棋盤格狀的8個1*1小正方形,可以發現他們使用到的火柴棒是互相獨立沒有交集的,
因此若要將這些小正方形完全破壞至少需要移除8根火柴棒。
注意另外一組8個1*1小正方形也是一樣的。其中位在最外圈的火柴棒都只有構成其中一種組合中的小正方形。
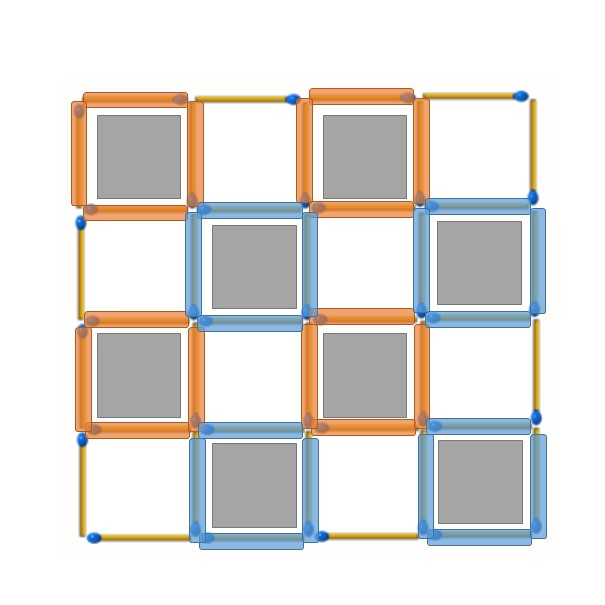
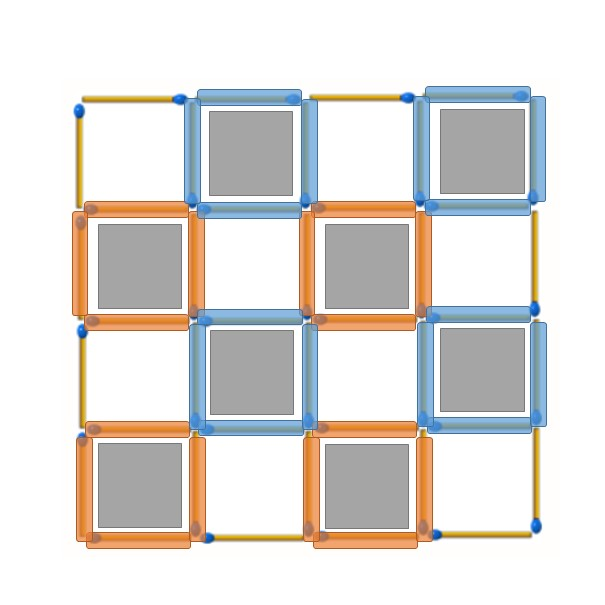
結合上面兩張圖可以發現,如果選擇移除了最外圈的火柴棒,我們就能找到一組小正方形還需要再移除8根火柴棒,總共會用到9根(以下圖來說,如果選擇移除橘色位置的火柴棒,那麼橘色的8個小正方形就會需要再移除至少8根火柴棒;而如果選擇移除藍色位置的火柴棒,藍色的8個小正方形就會需要再移除8根)。

但如果不移除最外圈的火柴棒,就代表會存在最大的4*4正方形沒有被破壞,仍然無法消除所有的正方形。
故得證至少要移除9根火柴棒才行。
那麼該如何找到一個只移除9根火柴棒的解呢?雖然這種組合最佳化問題有時是不容易取得最佳方案的,但因為這題的限制比較小(除了小正方形以外我們只需要對付9+4+1個2*2以上的正方形),我們可以試著「貪心」的選擇--挑選一些當下看起來能一次破壞很多正方形的火柴棒。
從上面的討論得知最外圈要恰好移除一根火柴棒。考慮對稱的情形其實只有兩種位置可以選擇:位在角落(藍色)的或者位在邊上(橘色)的位置。其中藍色火柴棒可以順帶破壞一個2*2的正方形和一個3*3的正方形;但如果選擇橘色的火柴棒還可以再破壞兩個橘色的大正方形,顯然選擇橘色的位置看起來是比較好的。
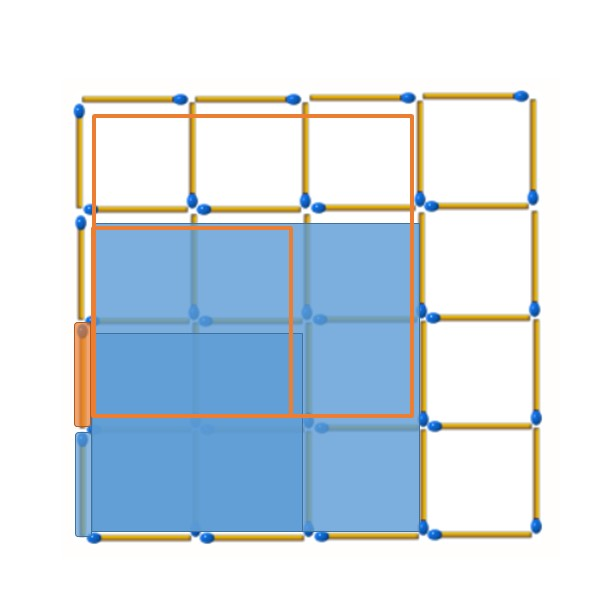
接著根據上面棋盤格的上色方式,我們可以得知每個橘色的1*1小正方形四邊都需要恰有一根被移除的火柴棒。考慮最左下角的小正方形,三個藍色位置火柴棒的位置都無法再破壞額外的正方形,但橘色的火柴棒可以順帶破壞1*1、2*2和3*3的正方形各一個,是比較好的選擇。之後藍色位置的火柴棒就不能再被移除了。
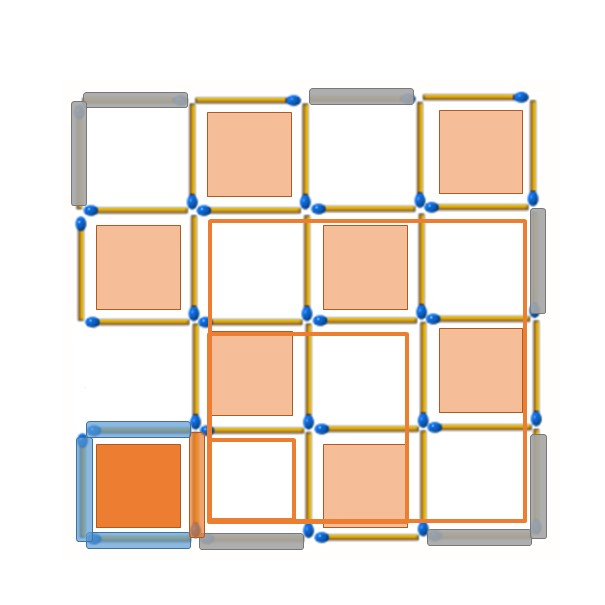
同樣考慮最左邊一直欄的1*1小正方形,藍色位置的火柴棒最多只能破壞一個2*2的正方形(最左上角),但橘色位置可以一次破壞兩個2*2的正方形和一個3*3的正方形,是比較有效率的選擇。移除完以後為了破壞最左上角的小正方形必須移除右圖橘色位置的火柴棒,接著右圖橘色的1*1小正方形另外三邊就被固定不能被移除了。
(到這裡已經沒有3*3和4*4的正方形了。)
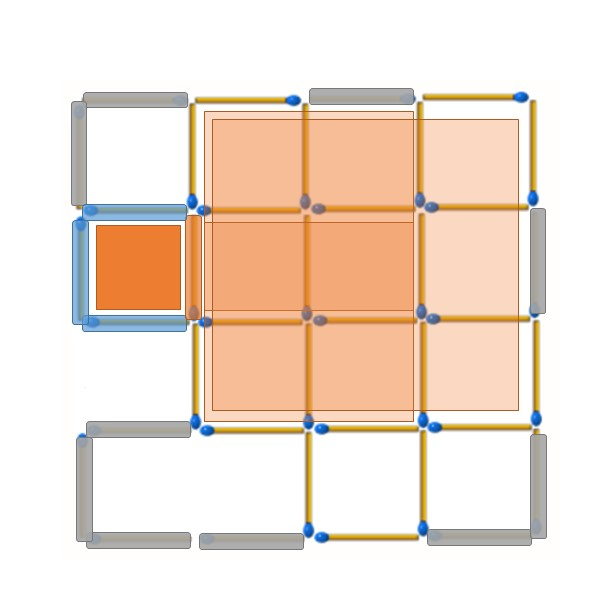
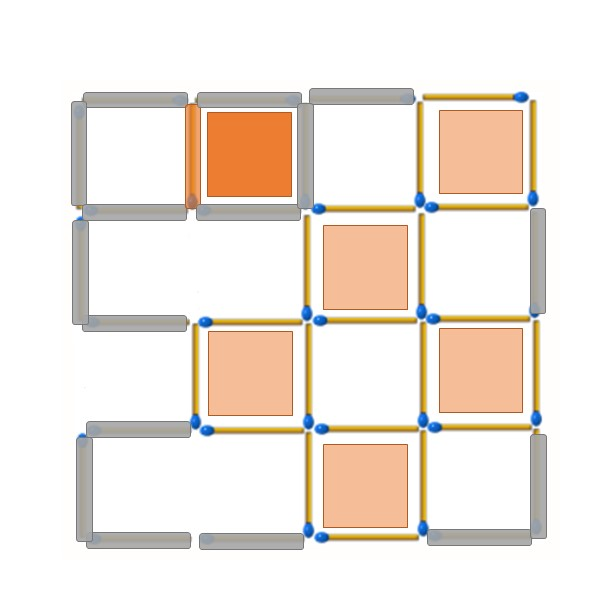
最左上角的2*2正方形還沒有被破壞,這次讓我們從該正方形考慮起。藍色位置的火柴棒無法順帶破壞任何正方形,但選擇橘色位置的火柴棒可以順帶再破壞兩個2*2小正方形,優先選擇移除橘色位置的火柴棒。
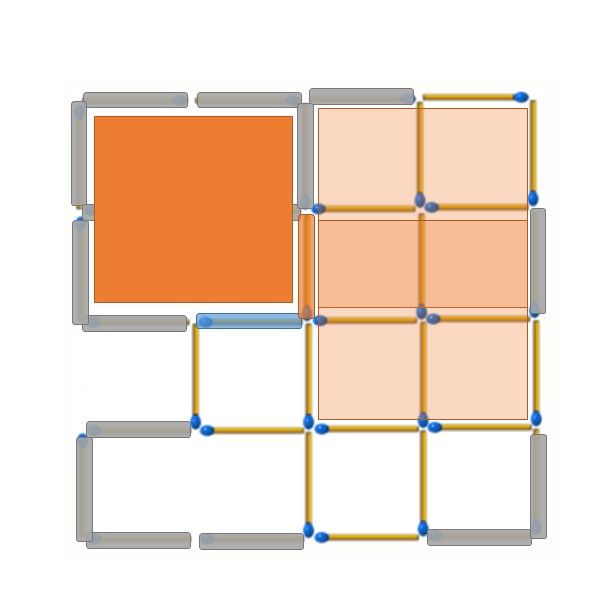
剩下的部分就像推骨牌一樣,每個位置A的1*1小正方形因為有一邊的火柴棒被移除了,剩下三邊都不能被移除;緊接著位置B的1*1小正方形因為有三邊的火柴棒不能被移除,只能移除剩下一邊橘色位置的火柴棒。
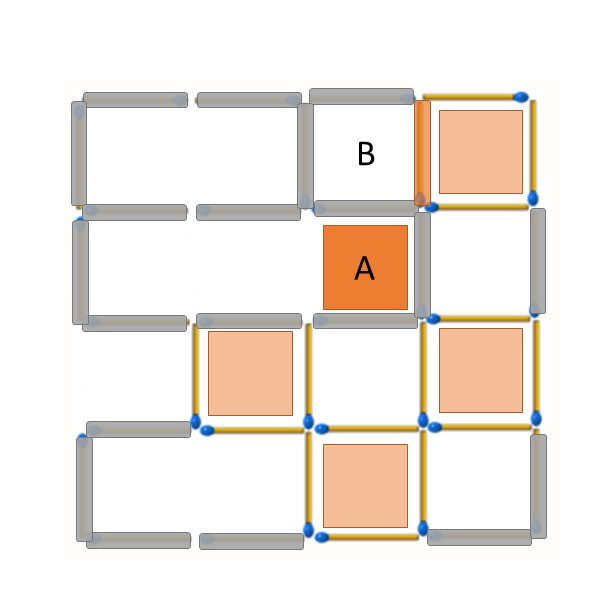
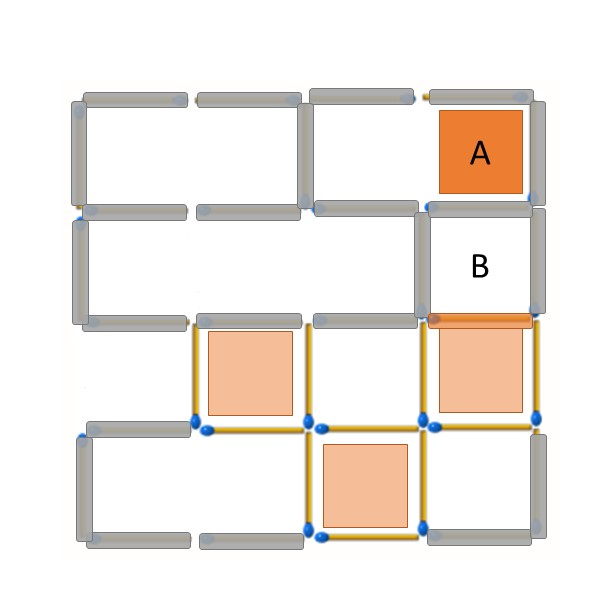
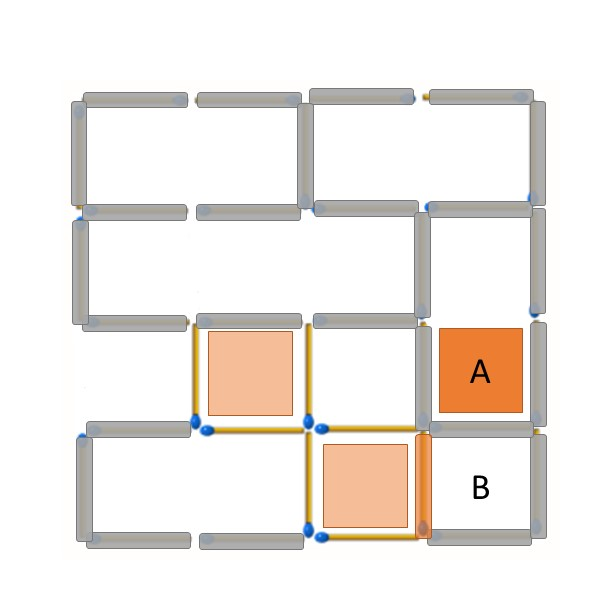
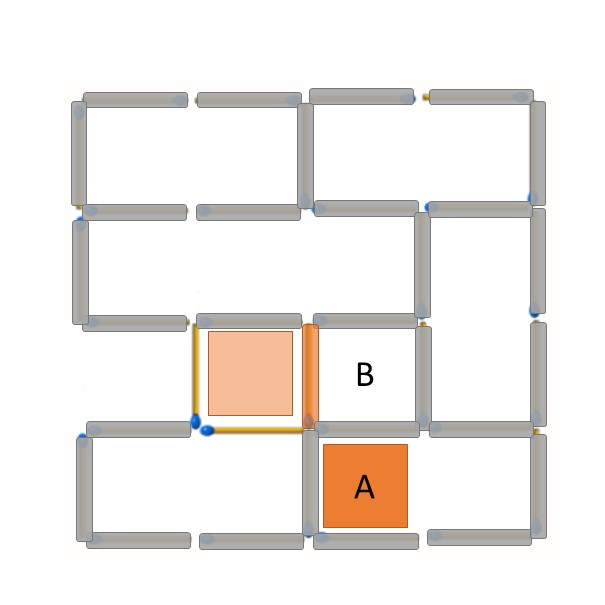
最後的結果即為一開始提供答案旋轉180度的情形:
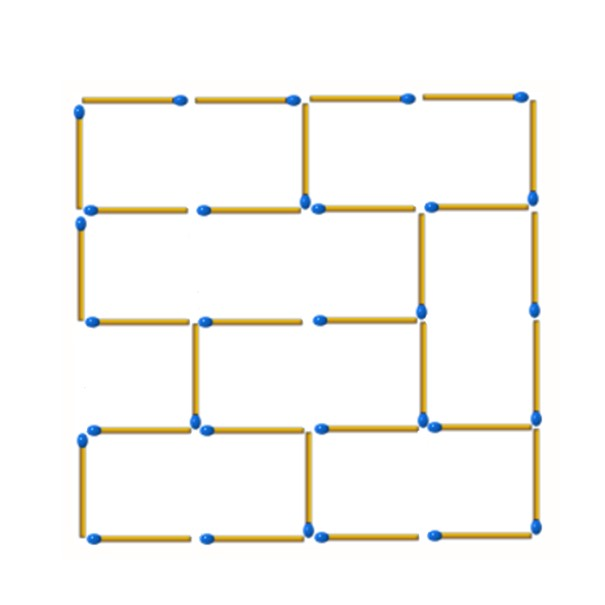
事實上,若將所有對稱形式的解視為相同,總共也只有2種作法。除了上述給的作法外另一種作法如下:
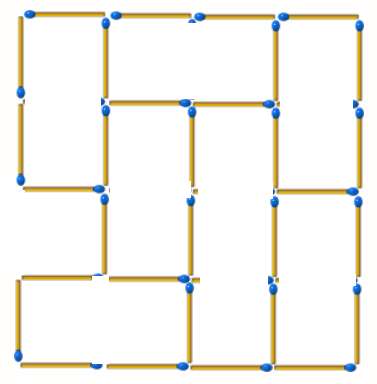

如何證明9根一定是最少呢?我們可以試著分析有沒有可能只移除8根火柴棒。
觀察如棋盤格狀的8個1*1小正方形,可以發現他們使用到的火柴棒是互相獨立沒有交集的,
因此若要將這些小正方形完全破壞至少需要移除8根火柴棒。
注意另外一組8個1*1小正方形也是一樣的。其中位在最外圈的火柴棒都只有構成其中一種組合中的小正方形。


結合上面兩張圖可以發現,如果選擇移除了最外圈的火柴棒,我們就能找到一組小正方形還需要再移除8根火柴棒,總共會用到9根(以下圖來說,如果選擇移除橘色位置的火柴棒,那麼橘色的8個小正方形就會需要再移除至少8根火柴棒;而如果選擇移除藍色位置的火柴棒,藍色的8個小正方形就會需要再移除8根)。

但如果不移除最外圈的火柴棒,就代表會存在最大的4*4正方形沒有被破壞,仍然無法消除所有的正方形。
故得證至少要移除9根火柴棒才行。
那麼該如何找到一個只移除9根火柴棒的解呢?雖然這種組合最佳化問題有時是不容易取得最佳方案的,但因為這題的限制比較小(除了小正方形以外我們只需要對付9+4+1個2*2以上的正方形),我們可以試著「貪心」的選擇--挑選一些當下看起來能一次破壞很多正方形的火柴棒。
從上面的討論得知最外圈要恰好移除一根火柴棒。考慮對稱的情形其實只有兩種位置可以選擇:位在角落(藍色)的或者位在邊上(橘色)的位置。其中藍色火柴棒可以順帶破壞一個2*2的正方形和一個3*3的正方形;但如果選擇橘色的火柴棒還可以再破壞兩個橘色的大正方形,顯然選擇橘色的位置看起來是比較好的。

接著根據上面棋盤格的上色方式,我們可以得知每個橘色的1*1小正方形四邊都需要恰有一根被移除的火柴棒。考慮最左下角的小正方形,三個藍色位置火柴棒的位置都無法再破壞額外的正方形,但橘色的火柴棒可以順帶破壞1*1、2*2和3*3的正方形各一個,是比較好的選擇。之後藍色位置的火柴棒就不能再被移除了。

同樣考慮最左邊一直欄的1*1小正方形,藍色位置的火柴棒最多只能破壞一個2*2的正方形(最左上角),但橘色位置可以一次破壞兩個2*2的正方形和一個3*3的正方形,是比較有效率的選擇。移除完以後為了破壞最左上角的小正方形必須移除右圖橘色位置的火柴棒,接著右圖橘色的1*1小正方形另外三邊就被固定不能被移除了。
(到這裡已經沒有3*3和4*4的正方形了。)


最左上角的2*2正方形還沒有被破壞,這次讓我們從該正方形考慮起。藍色位置的火柴棒無法順帶破壞任何正方形,但選擇橘色位置的火柴棒可以順帶再破壞兩個2*2小正方形,優先選擇移除橘色位置的火柴棒。

剩下的部分就像推骨牌一樣,每個位置A的1*1小正方形因為有一邊的火柴棒被移除了,剩下三邊都不能被移除;緊接著位置B的1*1小正方形因為有三邊的火柴棒不能被移除,只能移除剩下一邊橘色位置的火柴棒。




最後的結果即為一開始提供答案旋轉180度的情形:

事實上,若將所有對稱形式的解視為相同,總共也只有2種作法。除了上述給的作法外另一種作法如下:

11,914
上一道精選移動成立謎題
下一道精選移動成立謎題
 這題是快問快答,請先不要實際計算機率,看看你的直覺是正確的嗎?
兩個人猜拳,跟三個人猜拳,
哪一種比...
這題是快問快答,請先不要實際計算機率,看看你的直覺是正確的嗎?
兩個人猜拳,跟三個人猜拳,
哪一種比... 據報,一名走私販帶著大量現金搭上了特快車,
這班車中途都沒有停靠站,一路直達目的地,
警方隨即派人埋...
據報,一名走私販帶著大量現金搭上了特快車,
這班車中途都沒有停靠站,一路直達目的地,
警方隨即派人埋... 有一個人,他的夢想就是變成全世界最有錢的人,
一天,他走在路上突然碰到天使下凡,天使說:『我聽到你天...
有一個人,他的夢想就是變成全世界最有錢的人,
一天,他走在路上突然碰到天使下凡,天使說:『我聽到你天...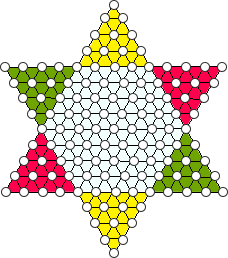 大家對跳棋應該都很熟悉,
棋盤長得像這樣:
棋盤上的圓圈都是可以放棋子的,
請問,棋盤上總共有多少...
大家對跳棋應該都很熟悉,
棋盤長得像這樣:
棋盤上的圓圈都是可以放棋子的,
請問,棋盤上總共有多少...